题目内容
(本题满分10分)如图是一个几何体的正视图和俯视图

(1)画出其侧视图,判断该几何体是什么几何体;
(2)求出该几何体的全面积和体积
(1)侧视图见解答,该几何体是一个正六棱锥.
(2)全面积为 ,体积为
,体积为 .
.
【解析】
试题分析:
(1)由俯视图可知该几何体底面是正六边形,结合正视图可知该几何体是一个正六棱锥.
(2)由正视图和俯视图可知该正六棱锥是由六个腰长是 ,底面边长是
,底面边长是 的等腰三角形与一个底面边长是
的等腰三角形与一个底面边长是 的正六边形围成,分别求出面积相加即得全面积为
的正六边形围成,分别求出面积相加即得全面积为 ,用勾股定理求出正六棱锥的高
,用勾股定理求出正六棱锥的高 ,再用
,再用 可求得体积为
可求得体积为 .
.
试题解析:
(1)左视图:见下图.可判断该几何体是一个正六棱锥(4分)

(2)正六棱锥的侧棱长是 ,底面边长是
,底面边长是 它是由六个腰长是
它是由六个腰长是 ,底面边长是
,底面边长是 的等腰三角形
的等腰三角形
与一个底面边长是 的正六边形围成∴
的正六边形围成∴
= =
= (7分)
(7分)
由正视图可知,正六棱锥的高 ,底面积
,底面积 ,∴
,∴ (10分)
(10分)
考点:1三视图;2几何体的表面积与体积.
考点分析: 考点1:三视图和直观图 考点2:柱、锥、台、球的表面积和体积 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
 在点A(e,1)处的切线斜率为 ( )
在点A(e,1)处的切线斜率为 ( ) D.
D.
 ,
, ,
, ,则下列不等式成立的是( )
,则下列不等式成立的是( ) B、
B、 C、
C、 D、
D、
 的单调递增区间为( )
的单调递增区间为( ) B.
B.
 D.
D.
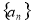 中,
中,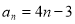 ,则首项
,则首项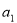 和公差
和公差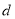 的值分别为( )
的值分别为( )  与
与 互相垂直,则
互相垂直,则
 ( )
( ) 上单调递增
上单调递增  ,
, 是双曲线
是双曲线
 ,
, 的左、右两个焦点,若双曲线右支上存在一点
的左、右两个焦点,若双曲线右支上存在一点 ,使
,使 (
( 为坐标原点),且
为坐标原点),且 ,则双曲线的离心率为( )
,则双曲线的离心率为( ) B.
B. C.
C. D.
D.