题目内容
一个正方体的体积是8,则这个正方体的内切球的表面积是( )
| A.8π | B.6π | C.4π | D.π |
C
解析试题分析:求出正方体的棱长,然后求出内切球的半径,即可求出灞桥区的表面积.正方体的体积为8,故边长为2,内切球的半径为1,则表面积 故选C
故选C
考点:棱柱的结构特征;球的体积和表面积.

练习册系列答案
相关题目
下列三个数: ,大小顺序正确的是( )
,大小顺序正确的是( )
A. | B. | C. | D. |
设 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 的最大值为6,则
的最大值为6,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
一个几何体的三视图如图所示,则该几何体的表面积和体积分别是
A.24+ 和40 和40 |
B.24+ 和72 和72 |
C.64+ 和40 和40 |
D.50+ 和72 和72 |
一只小球放入一长方体容器内,且与共点的三个面相接触.若小球上一点到这三个面的距离分别为4、5、5,则这只小球的半径是 ( )
| A.3或8 | B.8或11 | C.5或8 | D.3或11 |
设 是空间四个不同的点,在下列命题中,不正确的是( )
是空间四个不同的点,在下列命题中,不正确的是( )
A.若 与 与 共面,则 共面,则 与 与 共面 共面 |
B.若 与 与 是异面直线,则 是异面直线,则 与 与 是异面直线 是异面直线 |
C.若 ,则 ,则 |
D.若 ,则 ,则 |
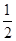 ,视图可以是,则该几何体的俯视图可以是( )
,视图可以是,则该几何体的俯视图可以是( )



 (a>0,b>0)的一条渐近线为
(a>0,b>0)的一条渐近线为 ,则它的离心率为( )
,则它的离心率为( )


