题目内容
已知｛an｝是首项为正数的等比数列，前n项和Sn=80，前2n项和S2n=6 560，在前n项中数值最大者为54，求通项an.
思路解析：若求an，则需求a1和公比q，这就需要列出关于a1和q的两个方程；另一方面，条件中所给“前n项中数值最大的是54”那么谁是最大的那一项？因此，还要根据公比q的取值来判断这个数列究竟是递增数列、递减数列，还是常数列或摆动数列. 解：∵Sn=80，S2n=6 560，显然公比q≠1， ∴ ∴qn=81，把它代入(1)中，得 而根据条件a1＞0，∴q＞1. 因此等比数列{an}是递增数列，前n项中数值最大的是an. ∴a1qn-1=54. 又qn=81，∴a1= 由 ∴an=2·3n-1. 深化升华 解决此题的关键是找出前n项中数值最大的项，这就需要判断数列的单调性.一般地，在等比数列中有a1＞0， a1＜0，
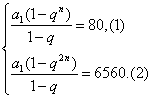
,得1+qn=82.
=80，即a1=q-1.
q.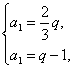
解得a1=2，q=3.
练习册系列答案
新目标检测同步单元测试卷系列答案
夺冠计划创新测评系列答案
概念地图系列答案
练习部分系列答案
课时测评导学导思导练系列答案
100分冲刺卷系列答案
初中单元期末卷系列答案
创新测试卷期末直通车系列答案
好卷100分系列答案
相关题目
已知a2010与a2011是首项为正数的等差数列{an}相邻的两项，且函数y=（x-a2010）（x-a2011）的图象如图所示，则使前n项和Sn＞0成立的最大自然数n是（ ）
，
…
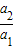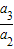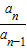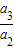…是首项为1，公比为2的等比数列，则数列{an}的第100项等于（ ）
，
…
…是首项为1，公比为2的等比数列，则数列{an}的第100项等于（ ）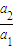
，
…
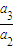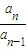…是首项为1，公比为2的等比数列，则数列{an}的第100项等于（ ）