题目内容
设![]() =0是函数
=0是函数![]() 的一个极值点.
的一个极值点.
(Ⅰ)求![]() 与
与![]() 的关系式(用
的关系式(用![]() 表示
表示![]() ,并求
,并求![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() >0,
>0,![]() (
(![]() )=
)=![]() ,问是否存在
,问是否存在![]() 、
、![]() 〔-2,2〕,使得
〔-2,2〕,使得![]() ≤l成立?若存在,求
≤l成立?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
解:(Ⅰ) ![]()
由![]() ,得
,得![]()
∴![]() ,
,![]()
令![]() ,得
,得![]() ,
,![]()
由于![]() 是
是![]() 极值点,故
极值点,故![]() ,即
,即![]()
当![]() 时,
时,![]() ,故
,故![]() 的单调增区间是
的单调增区间是![]() 和
和![]() ,单调减区间是
,单调减区间是![]()
当![]() 时,
时,![]() ,故
,故![]() 的单调增区间是
的单调增区间是![]() 和
和![]() ,单调减区间是
,单调减区间是![]()
(Ⅱ)当![]() 时,
时,![]() ,
,![]() 在[-2,0]上单调递减,在[0,2]上单调递增,
在[-2,0]上单调递减,在[0,2]上单调递增,
因此![]() 在[-2,2]上的值域为
在[-2,2]上的值域为![]()
而![]() 在[-2,2]上递减,所以值域
在[-2,2]上递减,所以值域![]()
因为在[-2,2]上![]()
所以,不存在![]() 、
、![]() 使得
使得![]() 成立
成立

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 时,f(x)取得极小值
时,f(x)取得极小值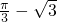 .
.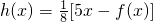 ,设x1是方程h(x)-x=0的实数根,若对于h(x)定义域中任意的x2、x3,当|x2-x1|<1,且|x3-x1|<1时,问是否存在一个最小的正整数M,使得|h(x3)-h(x2)|≤M恒成立,若存在请求出M的值;若不存在请说明理由.
,设x1是方程h(x)-x=0的实数根,若对于h(x)定义域中任意的x2、x3,当|x2-x1|<1,且|x3-x1|<1时,问是否存在一个最小的正整数M,使得|h(x3)-h(x2)|≤M恒成立,若存在请求出M的值;若不存在请说明理由.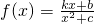 (c>0且c≠1,k>0)恰有一个极大值点和一个极小值点,且其中一个极值点是x=-c
(c>0且c≠1,k>0)恰有一个极大值点和一个极小值点,且其中一个极值点是x=-c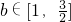 恒成立,求k的取值范围.
恒成立,求k的取值范围.