Question

平面内有n(n≥2)条直线,其中任何两条不平行,任何三条不过同一个点,证明交点的个数f(n)等于.

Answer 1

思路分析:本例的关键是弄清增加一条直线能够增加多少个不同的交点,解此类问题时常运用几何图形的性质.

证明:(1)当n=2时,两条直线的交点只有1个,又f(2)=×2×(2-1)=1,

因此,当n=2时,命题成立.

(2)假设当n=k(k≥2)时命题成立,就是说,平面内满足题设的任何k条直线的交点的个数f(k)= k(k-1).现在来考虑平面内有k+1条直线的情况.任取其中的1条直线,记为l(如图2-3-1).

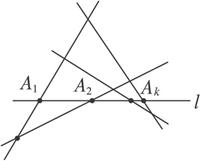
图2-3-1

由上面的假设,除l以外的其他k条直线的交点的个数为f(k)=k(k-1).另外,因为已知任何两条直线不平行,所以直线l必与平面内其他k条直线都相交(有k个交点);又因为已知任何三条直线不过同一点,所以上面的k个交点两两不同,且与平面内其他的k(k-1)个交点也两两不相同,从而平面内交点的个数为k(k-1)+k=k［(k-1)+2］

=(k+1)［(k+1)-1］.

这就是说,当n=k+1时,k+1条直线的交点个数f(k+1)=(k+1)［(k+1)-1］.

根据(1)(2),可知命题对任何大于1的正整数都成立.