Question

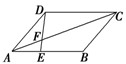
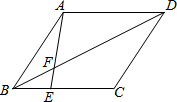如图所示，平行四边形ABCD中，E是BC边上一点，且BE=

1

2

EC，BD、AE相交于F点，
（1）求△BEF与△AFD的周长之比；
（2）若S_△BEF=6cm²，求S_△AFD．

Answer 1

分析：（1）利用平行四边形的性质、相似三角形的性质即可得出；
（2）利用相似三角形的性质：面积的比等于相似比的平方即可得出．

解答：解：（1）在平行四边形ABCD中，AD

∥

.

BC，
∴△BEF∽△AFD，
又∵BE=

1

2

EC，∴

BE

AD

=

BF

DF

=

EF

AF

=

1

3

．
∴△BEF与△AFD的周长之比=

BE+BF+EF

AD+DF+AF

=

1

3

．
（2）由（1）可知：△BEF∽△AFD，且相似比=

1

3

．
∴

S△BEF

S△AFD

=(

1

3

)2，
∴S_△AFD=9S_△BEF=9×6=54．

点评：本题考查了平行四边形的性质、相似三角形的性质，属于基础题．