Question

斜率为2的直线l被双曲线=1截得的弦长为4,求直线l的方程.

Answer 1

y=2x+或y=2x-

解析:

设直线l的方程式y=2x+m与双曲线交于A、B两点.

设A(x₁,y₁),B(x₂,y₂).

由方程组得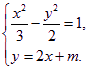

消去y,整理得10x²+12mx+3(m²+2)=0,

由判别式Δ=144m²-120(m²+2)=24m²-240＞0,

得m＞或m＜-.

由韦达定理知:x₁+x₂=-m,x₁x₂=(m²+2),

|AB|²=(1+k²)(x₁-x₂)²=5［(x₁+x₂)²-4x₁x₂］=m²-6(m²+2)=16,

化简得3m²=70,

∴m=±满足Δ＞0.

∴所求直线l的方程为

y=2x+或y=2x-.