题目内容
某同学参加北大、清华、科大三所学校的自主命题招生考试,其被录取的概率分别为
,
,
(各学校是否录取他相互独立,允许他可以被多个学校同时录取).
(1)求此同学没有被任何学校录取的概率;
(2)求此同学至少被两所学校录取的概率.
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
(1)求此同学没有被任何学校录取的概率;
(2)求此同学至少被两所学校录取的概率.
(1)该同学被北大,清华,科大录取分别记为事件A,B,C,
则该同学没有被任何学校录取记为事件D,且D=
.…(2分)
又∵
,
,
是相互独立的,…(3分)
∴P(D)=P(
)=P(
)P(
)P(
)=(1-
)×(1-
)×(1-
)=
×
×
=
.…(6分)
(2)设此同学至少被两所学校录取记为事件E,则E=ABC+AB
+A
C+
BC.…(9分)
∴P(E)=P(ABC)+P(AB
)+P(A
C)+P(
BC)=
×
×
+
×
×
+
×
×
+
×
×
=
.…(12分)
则该同学没有被任何学校录取记为事件D,且D=
| . |
| A |
| . |
| B |
| . |
| C |
又∵
| . |
| A |
| . |
| B |
| . |
| C |
∴P(D)=P(
| . |
| A |
| . |
| B |
| . |
| C |
| . |
| A |
| . |
| B |
| . |
| C |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
| 4 |
| 5 |
| 3 |
| 4 |
| 2 |
| 3 |
| 2 |
| 5 |
(2)设此同学至少被两所学校录取记为事件E,则E=ABC+AB
| . |
| C |
| . |
| B |
| . |
| A |
∴P(E)=P(ABC)+P(AB
| . |
| C |
| . |
| B |
| . |
| A |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
| 4 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
=
| 1 |
| 6 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (各学校是否录取他相互独立,允许他可以被多个学校同时录取).则此同学至少被两所学校录取的概率为_____.
(各学校是否录取他相互独立,允许他可以被多个学校同时录取).则此同学至少被两所学校录取的概率为_____.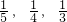 (各学校是否录取他相互独立,允许他可以被多个学校同时录取).
(各学校是否录取他相互独立,允许他可以被多个学校同时录取).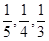 (各学校是否录取他相互独立,允许他可以被多个学校同时录取).
(各学校是否录取他相互独立,允许他可以被多个学校同时录取).