题目内容
某同学参加北大、清华、科大三所学校的自主命题招生考试,其被录取的概率分别为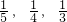 (各学校是否录取他相互独立,允许他可以被多个学校同时录取).
(各学校是否录取他相互独立,允许他可以被多个学校同时录取).
(1)求此同学没有被任何学校录取的概率;
(2)求此同学至少被两所学校录取的概率.
解:(1)该同学被北大,清华,科大录取分别记为事件A,B,C,
则该同学没有被任何学校录取记为事件D,且 .…(2分)
.…(2分)
又∵ 是相互独立的,…(3分)
是相互独立的,…(3分)
∴ =
= .…(6分)
.…(6分)
(2)设此同学至少被两所学校录取记为事件E,则 .…(9分)
.…(9分)
∴ =
=
= .…(12分)
.…(12分)
分析:(1)该同学被北大,清华,科大录取分别记为事件A,B,C,则该同学没有被任何学校录取记为事件D,则由 ,运算求得结果.
,运算求得结果.
(2)设此同学至少被两所学校录取记为事件E,再根据 ,运算求得结果.
,运算求得结果.
点评:本题主要考查相互独立事件的概率乘法公式的应用,体现了分类讨论的数学思想,属于基础题.
则该同学没有被任何学校录取记为事件D,且
 .…(2分)
.…(2分)又∵
 是相互独立的,…(3分)
是相互独立的,…(3分)∴
 =
= .…(6分)
.…(6分)(2)设此同学至少被两所学校录取记为事件E,则
 .…(9分)
.…(9分)∴
 =
=
=
 .…(12分)
.…(12分)分析:(1)该同学被北大,清华,科大录取分别记为事件A,B,C,则该同学没有被任何学校录取记为事件D,则由
 ,运算求得结果.
,运算求得结果.(2)设此同学至少被两所学校录取记为事件E,再根据
 ,运算求得结果.
,运算求得结果.点评:本题主要考查相互独立事件的概率乘法公式的应用,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
 (各学校是否录取他相互独立,允许他可以被多个学校同时录取).则此同学至少被两所学校录取的概率为_____.
(各学校是否录取他相互独立,允许他可以被多个学校同时录取).则此同学至少被两所学校录取的概率为_____.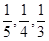 (各学校是否录取他相互独立,允许他可以被多个学校同时录取).
(各学校是否录取他相互独立,允许他可以被多个学校同时录取).