题目内容
数列{an}对任意n∈N*,满足an+1=an+1,a3=2.(1)求数列{an}通项公式;
(2)若
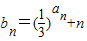 ,求{bn}的通项公式及前n项和.
,求{bn}的通项公式及前n项和.
【答案】分析:(1)由已知得an+1-an=1数列{an}是等差数列,且公差d=1,再由a3=2,求出首项,从而得到{an}通项公式.
(2)由(1)得,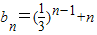 ,拆项后分别利用等比数列的前n项和公式以及等差数列的前n项和公式,运算求得结果.
,拆项后分别利用等比数列的前n项和公式以及等差数列的前n项和公式,运算求得结果.
解答:解:(1)由已知得an+1-an=1数列{an}是等差数列,且公差d=1.…(2分)
又a3=2,得a1=0,所以 an=n-1.…(4分)
(2)由(1)得,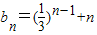 ,
,
所以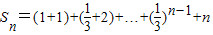 =
=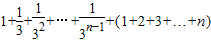 ,…(6分)
,…(6分)
故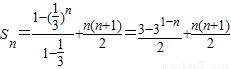 .…(12分)
.…(12分)
点评:本题主要考查等差数列的通项公式,前n项和公式,等比数列的前n项和公式及其应用,属于中档题.
(2)由(1)得,
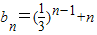 ,拆项后分别利用等比数列的前n项和公式以及等差数列的前n项和公式,运算求得结果.
,拆项后分别利用等比数列的前n项和公式以及等差数列的前n项和公式,运算求得结果.解答:解:(1)由已知得an+1-an=1数列{an}是等差数列,且公差d=1.…(2分)
又a3=2,得a1=0,所以 an=n-1.…(4分)
(2)由(1)得,
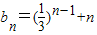 ,
,所以
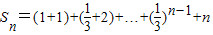 =
=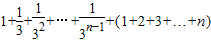 ,…(6分)
,…(6分)故
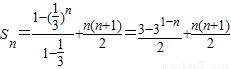 .…(12分)
.…(12分)点评:本题主要考查等差数列的通项公式,前n项和公式,等比数列的前n项和公式及其应用,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目