题目内容
1.已知A(x1,y1)是抛物线y2=4x上的一个动点,B(x2,y2)是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上的一个动点,N(1,0)是一定点,若AB∥x轴,且x1<x2,且△NAB的周长的取值范围是_($\frac{10}{3}$,4).分析 可考虑用抛物线的焦半径公式和椭圆的焦半径公式来做,先通过联立抛物线与椭圆方程,求出A,B点的横坐标范围,再利用焦半径公式转换为以B点的横坐标为参数的式子,再根据前面求出的B点横坐标范围计算即可.
解答 解: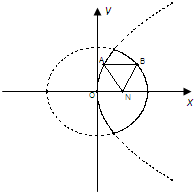 如图A,B分别在如图所示的实线运动,
如图A,B分别在如图所示的实线运动,
由$\left\{\begin{array}{l}{{y}^{2}=4x}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$得,抛物线y2=4x与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1
在第一象限的交点横坐标为$\frac{2}{3}$,
设A(x1,y1),B(x2,y2),
则0<x1<$\frac{2}{3}$,$\frac{2}{3}$<x2<2,
由可得,三角形ABN的周长l=|AN|+|AB|+|BN|
=x1+$\frac{p}{2}$+x2-x1+a-ex2
=$\frac{p}{2}$+a+$\frac{1}{2}$x2=3+$\frac{1}{2}$x2,
∵$\frac{2}{3}$<x2<2,
∴$\frac{10}{3}$<3+$\frac{1}{2}$x2<4,
故答案为:($\frac{10}{3}$,4).
点评 本题考查了抛物线与椭圆焦半径公式的应用,做题时要善于把未知转化为已知.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
9.设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x>0时,g(1)=0且f′(x)•g(x)+f(x)•g′(x)>0,则 不等式g(x)•f(x)>0的解集是( )
| A. | (-1,0)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
13.下列等式成立的是( )
| A. | ${∫}_{a}^{b}$0dx=b-a | B. | ${∫}_{a}^{b}$xdx=$\frac{1}{2}$ | ||
| C. | ${∫}_{-1}^{1}$|x|dx=2${∫}_{0}^{1}$|x|dx | D. | ${∫}_{a}^{b}$(x+1)dx=${∫}_{a}^{b}$xdx |