题目内容
我们可以利用数列{an}的递推公式an=
|
分析:借助于递推公式知道奇数项的值为其项数,而偶数项的值由对应的值来决定.又通过前面的项发现项的值为5时,下角码是首项为5,公比为2的等比数列.即可求出第8个5在该数列中所占的位置.
解答:解:由题得:这个数列各项的值分别为1,1,3,1,5,3,7,1,9,5,11,3…
∴a21+a25=21+25=46.
又因为a5=5,a10=5,a20=5,a40=5…
即项的值为5时,下角码是首项为5,公比为2的等比数列.
所以第8个5是该数列的第5×28-1=640项.
故答案为:46,640.
∴a21+a25=21+25=46.
又因为a5=5,a10=5,a20=5,a40=5…
即项的值为5时,下角码是首项为5,公比为2的等比数列.
所以第8个5是该数列的第5×28-1=640项.
故答案为:46,640.
点评:本题是对数列递推公式应用的考查.解题时要认真审题,仔细观察规律,避免错误.

练习册系列答案
相关题目
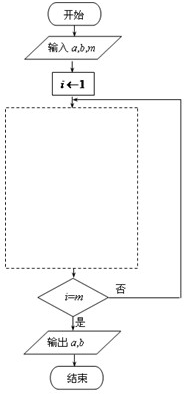 若数列{an},{bn}中,a1=a,b1=b,
若数列{an},{bn}中,a1=a,b1=b,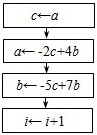 B、
B、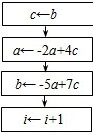
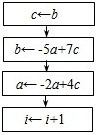 D、
D、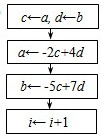
 (n≥2,n∈N*),且
(n≥2,n∈N*),且 .
.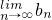 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明: 存在.
存在.