题目内容

在数列{an}中，已知a1=,a2=,且数列{an+1-an}是公比为12的等比数列，数列{lg（an+1-an）}是公差为-1的等差数列.

（1）求数列{an}的通项公式;

（2）Sn=a1+a2+…+an（n≥1）,求Sn.

 

解:（1）由{an+1-an}是公比为的等比数列，且a1=,a2=,

∴an+1-an=（-×）（）n-1=×（）n-1=.

∴an+1=an+                                                           ①

又由数列{lg（an+1-an）}是公差为-1的等差数列，且首项为lg（a2-a1）

=lg（-×）=-2.

∴lg（an+1-an）

=-2+（n-1）×（-1）=-（n+1）.

∴an+1-an=10,

即a n+1=an+10.                                                        ②

由①②联立解得

an=［（）n+1-（）n+1］.

（2）Sn=a1+a2+…+an

={-}.

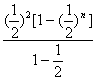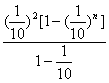∴Sn=［-］=.

练习册系列答案
相关题目
在数列{an}中，已知a1=
1
4
，
an+1
an
=
1
4
，bn+2=3log 
1
4
an（n∈N*）．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求证：数列{bn}是等差数列；
（Ⅲ）设cn=
3
bn•bn+1
，Sn是数列{cn}的前n项和，求使Sn＜
m
20
对所有n∈N*都成立的最小正整数m．
在数列{an}中，已知a1=1，an+1=
an1+2an
(n∈N+)．
（1）求a2，a3，a4，并由此猜想数列{an}的通项公式an的表达式；
（2）用适当的方法证明你的猜想．
在数列{an}中，已知a1=1，a2=2，且an+2等于an•an+1的个位数（n∈N*），若数列{an}的前k项和为2011，则正整数k之值为（　　）
（2012•淮南二模）在数列{an}中，已知an≥1，a1=1，且an+1-an=
2
an+1+an-1
，n∈N+．
（1）记bn=（an-
1
2
）2，n∈N+，求证：数列{bn}是等差数列；
（2）求{an}的通项公式；
（3）对?k∈N+，是否总?m∈N+使得an=k？若存在，求出m的值，若不存在，请说明理由．
在数列{an}中，已知a1=
7
2
，an=3an-1+3n-1（n≥2，n∈N*）．
（Ⅰ）计算a2，a3；
（Ⅱ）求证：{
an-
1
2
3n
}是等差数列；
（Ⅲ）求数列{an}的通项公式an及其前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网