Question

已知中心在坐标原点，焦点在轴上的椭圆过点，且它的离心率.

（Ⅰ）求椭圆的标准方程；

（Ⅱ）与圆相切的直线交椭圆于两点，若椭圆上一点满足，求实数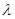的取值范围.

 

Answer 1

【答案】

(1) (2)

【解析】

试题分析：解：(Ⅰ) 设椭圆的标准方程为  1分

由已知得： 解得 ┈ 4分

所以椭圆的标准方程为：       5分

(Ⅱ) 因为直线：与圆相切

所以，       6分

把代入并整理得： ┈7分

设，则有 

     8分

因为，， 所以，┈┈ 9分

又因为点在椭圆上， 所以，   10分

                      12分

因为    所以                  13分

所以 ，所以 的取值范围为       14分

考点：椭圆的方程，直线与椭圆位置关系

点评：解决的关键是利用几何性质得到a,b,c的关系式求解方程，同时能联立方程组来得到根的关系，结合向量的坐标得到求解，属于基础题。