题目内容
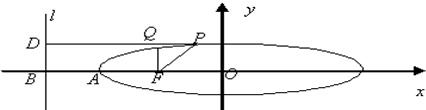
 如图所示:椭圆的中心为O,F为焦点,A为顶点,准线L交OA的延长线于B,P、Q在椭圆上,且PD⊥L于D,QF⊥OA于F,椭圆的离心率为e,给出下列结论:
如图所示:椭圆的中心为O,F为焦点,A为顶点,准线L交OA的延长线于B,P、Q在椭圆上,且PD⊥L于D,QF⊥OA于F,椭圆的离心率为e,给出下列结论:
① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤
其中正确命题的序号是________(写出所有正确命题的序号)
①②③⑤
分析:根据题意,设椭圆的方程为 +
+ =1,进而由椭圆的方程,分别化简表示、计算5个式子的值,与离心率e=
=1,进而由椭圆的方程,分别化简表示、计算5个式子的值,与离心率e= 比较可得答案.
比较可得答案.
解答:设椭圆的方程为 +
+ =1,(0<a<b)依次分析5个比值的式子可得:
=1,(0<a<b)依次分析5个比值的式子可得:
①、根据椭圆的第二定义,可得 =e,故符合;
=e,故符合;
②、根据椭圆的性质,可得|BF|= -c=
-c= ,|QF|=
,|QF|= ,则
,则  =
= =e,故符合;
=e,故符合;
③、由椭圆的性质,可得|AO|=a,|BO|= ,则
,则  =
= =e,故符合;
=e,故符合;
④、由椭圆的性质,可得|AF|=a-c, =e|AF|≠|PD|,故不符合;
=e|AF|≠|PD|,故不符合;
⑤、由椭圆的性质,可得|AO|=a,|FO|=c, =
= =e,故符合;
=e,故符合;
故答案为①②③⑤.
点评:题考查椭圆的性质,需要掌握椭圆的常见性质以及其中的一些特殊的长度,如|BF|= -c=
-c= ,是焦准距.
,是焦准距.
分析:根据题意,设椭圆的方程为
 +
+ =1,进而由椭圆的方程,分别化简表示、计算5个式子的值,与离心率e=
=1,进而由椭圆的方程,分别化简表示、计算5个式子的值,与离心率e= 比较可得答案.
比较可得答案.解答:设椭圆的方程为
 +
+ =1,(0<a<b)依次分析5个比值的式子可得:
=1,(0<a<b)依次分析5个比值的式子可得:①、根据椭圆的第二定义,可得
 =e,故符合;
=e,故符合;②、根据椭圆的性质,可得|BF|=
 -c=
-c= ,|QF|=
,|QF|= ,则
,则  =
= =e,故符合;
=e,故符合;③、由椭圆的性质,可得|AO|=a,|BO|=
 ,则
,则  =
= =e,故符合;
=e,故符合;④、由椭圆的性质,可得|AF|=a-c,
 =e|AF|≠|PD|,故不符合;
=e|AF|≠|PD|,故不符合;⑤、由椭圆的性质,可得|AO|=a,|FO|=c,
 =
= =e,故符合;
=e,故符合;故答案为①②③⑤.
点评:题考查椭圆的性质,需要掌握椭圆的常见性质以及其中的一些特殊的长度,如|BF|=
 -c=
-c= ,是焦准距.
,是焦准距. 
练习册系列答案
相关题目
 如图所示:椭圆的中心为O,F为焦点,A为顶点,准线L交OA的延长线于B,P、Q在椭圆上,且PD⊥L于D,QF⊥OA于F,椭圆的离心率为e,给出下列结论:
如图所示:椭圆的中心为O,F为焦点,A为顶点,准线L交OA的延长线于B,P、Q在椭圆上,且PD⊥L于D,QF⊥OA于F,椭圆的离心率为e,给出下列结论: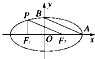 如图所示,椭圆的中心在原点,焦点F1、F2在x轴上,A、B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,则此椭圆的离心率是( )
如图所示,椭圆的中心在原点,焦点F1、F2在x轴上,A、B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,则此椭圆的离心率是( )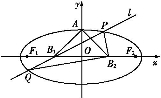
 ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤
