题目内容
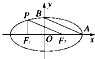 如图所示,椭圆的中心在原点,焦点F1、F2在x轴上,A、B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,则此椭圆的离心率是( )
如图所示,椭圆的中心在原点,焦点F1、F2在x轴上,A、B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,则此椭圆的离心率是( )分析:由PF1⊥x轴,先求出点P的坐标,再由PF2∥AB,能得到b=2c,由此能求出椭圆的离心率.
解答:解: 如图,∵PF1⊥x轴,∴点P的坐标(-c,
如图,∵PF1⊥x轴,∴点P的坐标(-c,
),
kAB=-
,kPF2=-
,
∵PF2∥AB,
∴kAB=kPF2,即-
=-
,
整理,得b=2c,
∴a2=b2+c2=5c2,即a=
c,
∴e=
=
.
故选B.
 如图,∵PF1⊥x轴,∴点P的坐标(-c,
如图,∵PF1⊥x轴,∴点P的坐标(-c,| b2 |
| a |
kAB=-
| b |
| a |
| b2 |
| 2ac |
∵PF2∥AB,
∴kAB=kPF2,即-
| b |
| a |
| b2 |
| 2ac |
整理,得b=2c,
∴a2=b2+c2=5c2,即a=
| 5 |
∴e=
| c |
| a |
| ||
| 5 |
故选B.
点评:本题考查椭圆的离心率,解题时要熟练掌握椭圆的简单性质,注意两直线平行斜率相等的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
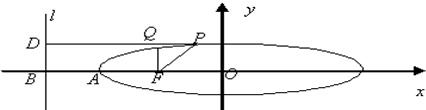 如图所示:椭圆的中心为O,F为焦点,A为顶点,准线L交OA的延长线于B,P、Q在椭圆上,且PD⊥L于D,QF⊥OA于F,椭圆的离心率为e,给出下列结论:
如图所示:椭圆的中心为O,F为焦点,A为顶点,准线L交OA的延长线于B,P、Q在椭圆上,且PD⊥L于D,QF⊥OA于F,椭圆的离心率为e,给出下列结论: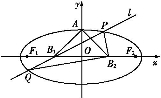
 如图所示:椭圆的中心为O,F为焦点,A为顶点,准线L交OA的延长线于B,P、Q在椭圆上,且PD⊥L于D,QF⊥OA于F,椭圆的离心率为e,给出下列结论:
如图所示:椭圆的中心为O,F为焦点,A为顶点,准线L交OA的延长线于B,P、Q在椭圆上,且PD⊥L于D,QF⊥OA于F,椭圆的离心率为e,给出下列结论: ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤
 ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤
