题目内容
已知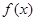 是以
是以 为周期的偶函数,且
为周期的偶函数,且 时,
时, ,则当
,则当 时,
时,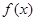 等于 ( )
等于 ( )
A. | B. | C. | D. |
B
解析试题分析:由题意,任取
又f(x)是偶函数,可得f(-x)=f(x)∴x∈ 时,函数解析式为f(x)=1+sinx
时,函数解析式为f(x)=1+sinx
由于f(x)是以π为周期的函数,任取 ,则
,则 ,∴f(x)=f(x-3π)=1+sin(x-3π)=1-sinx,故选B
,∴f(x)=f(x-3π)=1+sin(x-3π)=1-sinx,故选B
考点:函数奇偶性
点评:解决的关键是对于函数周期性和奇偶性的熟练的运用,属于基础题。

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
使函数
 为增函数的区间是( )
为增函数的区间是( )
A. | B. | C. | D. |
 ( )
( )
A. | B. | C. | D. |
下列关系式中正确的是( )
A. | B. |
C. | D. |
若函数 是偶函数,则
是偶函数,则 的值可以是( )
的值可以是( )
A. | B. | C. | D. |
要得到函数 的图象,只要将函数
的图象,只要将函数 的图象( )
的图象( )
A.向左平移 单位 单位 | B.向右平移 单位 单位 |
C.向左平移 单位 单位 | D.向右平移 单位 单位 |
如果对于函数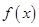 定义域内任意的
定义域内任意的 ,都有
,都有 (
( 为常数),称
为常数),称 为
为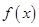 的下界,下界
的下界,下界 中的最大值叫做
中的最大值叫做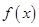 的下确界.下列函数中,有下确界的函数是( ).).
的下确界.下列函数中,有下确界的函数是( ).).
① ②
② ③
③ ④
④
| A.①② | B.①③ | C.②③④ | D.①③④ |
若函数 的图象(部分)如图所示,则
的图象(部分)如图所示,则 的取值是( )
的取值是( )
A. | B. |
C. | D. |
 )+
)+ 是奇函数,且在[0,
是奇函数,且在[0, 上是减函数的
上是减函数的


