题目内容
已知一直线通过点（-2，2），且与两坐标轴所围成的三角形的面积为1，求这条直线的方程．
解：设直线方程为y-2=k（x+2），令x=0得y=2k+2，令y=0得x=-2-
，
由题设条件
|-2-|•|2k+2|=1，
∴2（k+1）2=|k|，
∴
或
，
∴k=-2或-，
∴所求直线方程为：2x+y+2=0或x+2y-2=0．
分析：先设出直线的点斜式方程，求出直线在坐标轴上的截距，表示出三角形的面积，即可求出其斜率，进而求出直线的方程．
点评：熟练掌握直线的点斜式方程、三角形的面积计算公式、分类讨论的思想方法是解题的关键．
，由题设条件
|-2-|•|2k+2|=1，∴2（k+1）2=|k|，
∴
或，∴k=-2或-
，∴所求直线方程为：2x+y+2=0或x+2y-2=0．
分析：先设出直线的点斜式方程，求出直线在坐标轴上的截距，表示出三角形的面积，即可求出其斜率，进而求出直线的方程．
点评：熟练掌握直线的点斜式方程、三角形的面积计算公式、分类讨论的思想方法是解题的关键．
练习册系列答案
相关题目
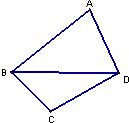已知一颗粒子等可能地落入如图所示的四边形ABCD内的任意位置，如果通过大量的实验发现粒子落入△BCD内的频率稳定在
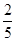附近，那么点A和点C到直线BD的距离之比约为 