题目内容
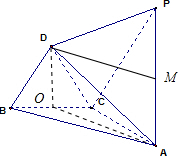
 已知△ABC与△DBC都是边长为2的等边三角形,且平面ABC⊥平面DBC,过点A作PA⊥平面ABC,且AP=2
已知△ABC与△DBC都是边长为2的等边三角形,且平面ABC⊥平面DBC,过点A作PA⊥平面ABC,且AP=2| 3 |
(1)求证:PA∥平面DBC;
(2)求直线DA与平面ABC所成角的大小.
分析:(1)取BC的中点O,连接DO,由等腰三角形三线合一的性质可得DO⊥BC,结合已知中平面ABC⊥平面DBC,PA⊥平面ABC,利用面面垂直的性质,及线面垂直的性质,可得DO∥PA,进而根据线面平行的判定定理,得到PA∥平面DBC;
(2)由(1)中结论,可得D在平面ABC的射影是O,P在平面ABC的射影是A,过D作DM∥OA交PA于M,则∠PDM等于直线PD与平面ABC所成角,解三角形PDM即可得到答案.
(2)由(1)中结论,可得D在平面ABC的射影是O,P在平面ABC的射影是A,过D作DM∥OA交PA于M,则∠PDM等于直线PD与平面ABC所成角,解三角形PDM即可得到答案.
解答:证明:(1)取BC的中点O,连接DO,则DO⊥BC
又∵平面DBC⊥平面ABC,
∴DO⊥平面ABC.
而AP⊥平面ABC,
∴DO∥PA,
又∵DO在平面DBC内,
∴PA∥平面DBC.
(2)∵D在平面ABC的射影是O,P在平面ABC的射影是A,
∴DP在平面ABC的射影是OA,即直线PD与平面ABC所成角就是直线PD与直线OA所成的角,
过D作DM∥OA交PA于M,
由(1)可知DO∥PA,
∴DM=OA=1,DO=MA=1⇒PM=1
∴cos∠PDM=
=
即∠PDM=45°

又∵平面DBC⊥平面ABC,
∴DO⊥平面ABC.
而AP⊥平面ABC,
∴DO∥PA,
又∵DO在平面DBC内,
∴PA∥平面DBC.
(2)∵D在平面ABC的射影是O,P在平面ABC的射影是A,
∴DP在平面ABC的射影是OA,即直线PD与平面ABC所成角就是直线PD与直线OA所成的角,
过D作DM∥OA交PA于M,
由(1)可知DO∥PA,
∴DM=OA=1,DO=MA=1⇒PM=1
∴cos∠PDM=
| DM |
| PD |
| ||
| 2 |
即∠PDM=45°
点评:本题考查的知识点是直线与平面所成的角,直线与平面平行的判定,其中(1)的关键是证得DO∥PA,(2)的关键是证得∠PDM等于直线PD与平面ABC所成角.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使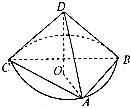 已知四面体ABCD中,DA=DB=DC=3
已知四面体ABCD中,DA=DB=DC=3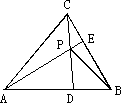
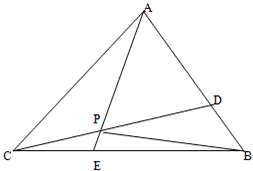 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使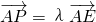 ,
,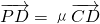 ,
,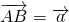 ,
,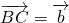 .
. ,
, 表示
表示 ;
;