题目内容
若椭圆
（a＞b＞0）过点（-3，2），离心率为
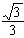，⊙O的圆心为原点，直径为椭圆的短轴，⊙M的方程为（x-8）2+（y-6）2=4，过⊙M上任一点P作⊙O的切线PA、PB，切点为A、B。
（1）求椭圆的方程；
（2）若直线PA与⊙M的另一交点为Q，当弦PQ最大时，求直线PA的直线方程；
（3）求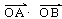
的最大值与最小值。
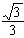（a＞b＞0）过点（-3，2），离心率为，⊙O的圆心为原点，直径为椭圆的短轴，⊙M的方程为（x-8）2+（y-6）2=4，过⊙M上任一点P作⊙O的切线PA、PB，切点为A、B。（1）求椭圆的方程；
（2）若直线PA与⊙M的另一交点为Q，当弦PQ最大时，求直线PA的直线方程；
（3）求
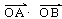的最大值与最小值。解：（1）由题意得
∴
所以椭圆的方程为
；
（2）由题可知当直线PA过圆M的圆心（8，6）时，弦PQ最大，因为直线PA的斜率一定存在
设直线PA的方程为：y-6=k（x-8）
又因为PA与圆O相切
所以圆心
到直线PA的距离为
即
可得直径PA的方程为
或
；
（3）设
则
则
∵
∴
∴
。
∴
所以椭圆的方程为
；（2）由题可知当直线PA过圆M的圆心（8，6）时，弦PQ最大，因为直线PA的斜率一定存在
设直线PA的方程为：y-6=k（x-8）
又因为PA与圆O相切
所以圆心
到直线PA的距离为即
可得直径PA的方程为
或；（3）设
则
则
∵
∴
∴
。
练习册系列答案
相关题目
=1(a＞b＞0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成5∶3两段,则此椭圆的离心率为( )
B.
C.
D.
=1(a＞b＞0)的左右焦点分别为F1、F2，线段F1F2被y2=2bx的焦点分成5：3的两段，则此椭圆的离心率为( )
B.
C.
D.
=1(a＞b＞0)与直线l: x+y=1在第一象限内有两个不同的交点，求a、b所满足的条件，并画出点P(a,b)的存在区域. 
（a>b>0）的离心率e＝
，则双曲线
离心率为
B. 
C.
D.
=1(a＞b＞0)与直线
在第一象限内有两个不同的交点，求a、b所满足的条件，并画出点P(a,b)的存在区域。