题目内容
在直角坐标平面中,△ABC的两个顶点A,B的坐标分别为A(-1,0)B(1,0),平面内两点G,M同时满足下列条件:①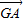 +
+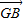 +
+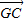 =
=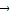 ;②|
;②|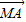 |=|
|=|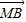 |=|
|=|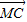 |;③
|;③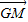 ∥
∥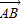 .
.(1)求△ABC的顶点C的轨迹方程;
(2)过点P(3,0)的直线l与(1)中轨迹交于不同的两点E,F,求△OEF面积的最大值.
【答案】分析:(1)分别设出点C、G、M的坐标,利用条件|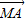 |=|
|=|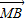 |求出M的横坐标,结合
|求出M的横坐标,结合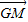 ∥
∥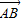 可得G和M的纵坐标相等,然后利用
可得G和M的纵坐标相等,然后利用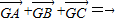 把G和M的坐标用C的坐标表示,代入|
把G和M的坐标用C的坐标表示,代入|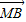 |=|
|=|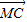 |即可得到C的轨迹方程;
|即可得到C的轨迹方程;
(2)设出直线l的方程,和椭圆方程联立后化为关于x的一元二次方程,利用根与系数关系得到E、F两点的横坐标的和与积,写出面积后得到关于直线斜率k的表达式,利用换元法降幂,然后利用导数求最值.
解答:(1)解:设C(x,y),G(x,y),M(xM,yM).
∵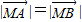 ,
,
∴M点在线段AB的中垂线上.由已知A(-1,0),B(1,0),∴xM=0.
又∵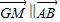 ,∴yM=y.又
,∴yM=y.又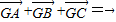 ,
,
∴(-1-x,-y)+(1-x,-y)+(x-x,y-y)=(0,0)
∴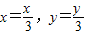 ,∴
,∴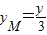 .
.
∵|MB|=|MC|,∴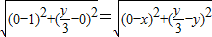 ,
,
∴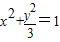 (y≠0),∴顶点C轨迹方程为
(y≠0),∴顶点C轨迹方程为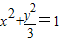 (y≠0).
(y≠0).
(2)设直线l方程为:y=k(x-3)(k≠0),E(x1,y1),F(x2,y2),
由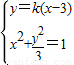 ,消去y得:(k2+3)x2-6k2x+9k2-3=0 ①
,消去y得:(k2+3)x2-6k2x+9k2-3=0 ①
∴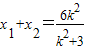 ,
,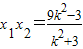 .
.
由方程①知△=(6k2)2-4(k2+3)(9k2-3)>0,
∴k2< ,∵k≠0,∴0<k2<
,∵k≠0,∴0<k2< .
.
而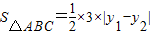 =
=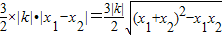
=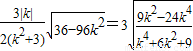 .
.
令k2=t,则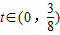 ,
,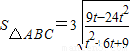 .记
.记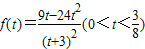 ,
,
求导后可得当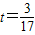 时△OEF面积有最大值为
时△OEF面积有最大值为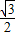 .
.
点评:本题考查了向量在几何中的应用,是直线与圆锥曲线的综合题,训练了“设而不求”的解题思想方法,训练了换元法,考查了导数在求最值中的作用,该题涉及条件多,解答的关键是找准入手点,是有一定难度题目.
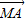 |=|
|=|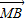 |求出M的横坐标,结合
|求出M的横坐标,结合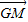 ∥
∥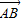 可得G和M的纵坐标相等,然后利用
可得G和M的纵坐标相等,然后利用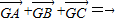 把G和M的坐标用C的坐标表示,代入|
把G和M的坐标用C的坐标表示,代入|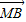 |=|
|=|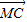 |即可得到C的轨迹方程;
|即可得到C的轨迹方程;(2)设出直线l的方程,和椭圆方程联立后化为关于x的一元二次方程,利用根与系数关系得到E、F两点的横坐标的和与积,写出面积后得到关于直线斜率k的表达式,利用换元法降幂,然后利用导数求最值.
解答:(1)解:设C(x,y),G(x,y),M(xM,yM).
∵
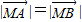 ,
,∴M点在线段AB的中垂线上.由已知A(-1,0),B(1,0),∴xM=0.
又∵
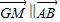 ,∴yM=y.又
,∴yM=y.又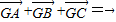 ,
,∴(-1-x,-y)+(1-x,-y)+(x-x,y-y)=(0,0)
∴
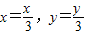 ,∴
,∴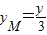 .
. ∵|MB|=|MC|,∴
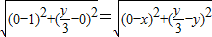 ,
,∴
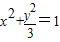 (y≠0),∴顶点C轨迹方程为
(y≠0),∴顶点C轨迹方程为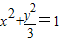 (y≠0).
(y≠0).(2)设直线l方程为:y=k(x-3)(k≠0),E(x1,y1),F(x2,y2),
由
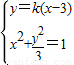 ,消去y得:(k2+3)x2-6k2x+9k2-3=0 ①
,消去y得:(k2+3)x2-6k2x+9k2-3=0 ①∴
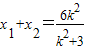 ,
,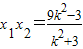 .
. 由方程①知△=(6k2)2-4(k2+3)(9k2-3)>0,
∴k2<
 ,∵k≠0,∴0<k2<
,∵k≠0,∴0<k2< .
. 而
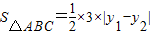 =
=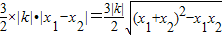
=
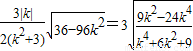 .
.令k2=t,则
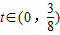 ,
,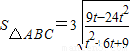 .记
.记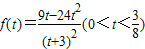 ,
,求导后可得当
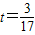 时△OEF面积有最大值为
时△OEF面积有最大值为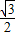 .
.点评:本题考查了向量在几何中的应用,是直线与圆锥曲线的综合题,训练了“设而不求”的解题思想方法,训练了换元法,考查了导数在求最值中的作用,该题涉及条件多,解答的关键是找准入手点,是有一定难度题目.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目