题目内容
已知函数
，当它的函数值大于零时，该函数的单调递增区间是
- A.
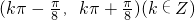
- B.
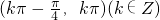
- C.
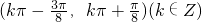
- D.
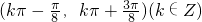
A
分析：利用y=sinx大于零的单调递增区间是：（2kπ，2kπ+
） k∈Z，解不等式 2kπ＜2x+
＜2kπ+，k∈Z；即求出函数的增区间．
解答：因为：y=sinx大于零的单调递增区间是：（2kπ，2kπ+） k∈Z
所以：2kπ＜2x+＜2kπ+，k∈Z．
得：kπ-
＜x＜kπ+，k∈Z．
故：函数，大于零的单调递增区间是：（kπ-，kπ+），k∈Z
故选：A．
点评：本题考查了正弦函数的单调性的应用，对于形如y=sin（ωx+φ）的性质，需要把“ωx+φ”作为一个整体，再利用正弦函数的单调性进行求解，考查了整体思想．
分析：利用y=sinx大于零的单调递增区间是：（2kπ，2kπ+
） k∈Z，解不等式 2kπ＜2x+＜2kπ+，k∈Z；即求出函数的增区间．解答：因为：y=sinx大于零的单调递增区间是：（2kπ，2kπ+
） k∈Z所以：2kπ＜2x+
＜2kπ+，k∈Z．得：kπ-
＜x＜kπ+，k∈Z．故：函数
，大于零的单调递增区间是：（kπ-，kπ+），k∈Z故选：A．
点评：本题考查了正弦函数的单调性的应用，对于形如y=sin（ωx+φ）的性质，需要把“ωx+φ”作为一个整体，再利用正弦函数的单调性进行求解，考查了整体思想．
练习册系列答案
相关题目
(x＞0)和定义在R上的奇函数g(x)，当x＞0时，g(x)=f(x)，试求g(x)的表达式和它的反函数．
，当它的函数值大于零时，该函数的单调递增区间是（ ）
