题目内容
如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF=1，则四面体A-EFB的体积为 ．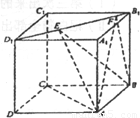
【答案】分析：计算三角形BEF的面积和A到平面BEF的距离，即可求出所求几何体的体积．
解答：解：由题意可知，由于点B到直线B1D1的距离不变，故△BEF的面积为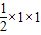
=
．
又点A到平面BEF的距离为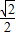
，故VA-BEF=
=
．
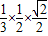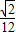故答案为：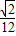
．
点评：本题考查几何体的体积的求法，考查计算能力．
解答：解：由题意可知，由于点B到直线B1D1的距离不变，故△BEF的面积为
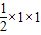=．又点A到平面BEF的距离为
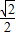，故VA-BEF=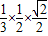=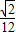．故答案为：
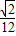．点评：本题考查几何体的体积的求法，考查计算能力．
练习册系列答案
中考解读考点精练系列答案
相关题目
如图，正方体ABCD-A1B1C1D1中，E，F分别为BB1和A1D1的中点．证明：向量
如图，正方体ABCD-A1B1C1D1棱长为8，E、F分别为AD1，CD1中点，G、H分别为棱DA，DC上动点，且EH⊥FG．
如图，正方体ABCD-A1B1C1D1中，若E、F、G分别为棱BC、C1C、B1C1的中点，O1、O2分别为四边形ADD1A1、A1B1C1D1的中心，则下列各组中的四个点不在同一个平面上的是（ ）
如图，正方体ABCD-A1B1C1D1中，E、F、G、H分别是所在棱的三等分点，且