题目内容
对于函数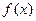 ,若存在
,若存在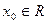 ,使
,使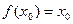 成立,则称点
成立,则称点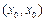 为函数的不动点。
为函数的不动点。
(1)已知函数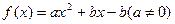 有不动点(1,1)和(-3,-3)求
有不动点(1,1)和(-3,-3)求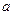 与
与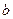 的值;
的值;
(2)若对于任意实数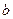 ,函数
,函数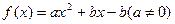 总有两个相异的不动点,求
总有两个相异的不动点,求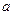 的取值范围;
的取值范围;
(3)若定义在实数集R上的奇函数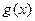 存在(有限的)
存在(有限的)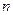 个不动点,求证:
个不动点,求证: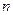 必为奇数。
必为奇数。
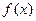 ,若存在
,若存在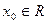 ,使
,使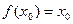 成立,则称点
成立,则称点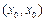 为函数的不动点。
为函数的不动点。(1)已知函数
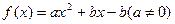 有不动点(1,1)和(-3,-3)求
有不动点(1,1)和(-3,-3)求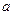 与
与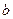 的值;
的值;(2)若对于任意实数
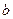 ,函数
,函数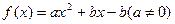 总有两个相异的不动点,求
总有两个相异的不动点,求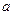 的取值范围;
的取值范围;(3)若定义在实数集R上的奇函数
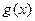 存在(有限的)
存在(有限的)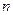 个不动点,求证:
个不动点,求证: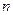 必为奇数。
必为奇数。(1)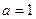 ,
,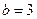 (2)
(2) (3)见解析
(3)见解析
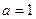 ,
,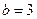 (2)
(2) (3)见解析
(3)见解析(1)由不动点的定义: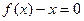 ,∴
,∴ …….1’
…….1’
代入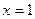 知
知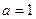 ,又由
,又由 及
及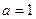 知
知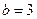 。……………………...2’
。……………………...2’
∴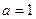 ,
,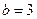 。 …………………………....................1’
。 …………………………....................1’
(2)对任意实数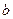 ,
,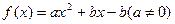 总有两个相异的不动点,即是对任意的实数
总有两个相异的不动点,即是对任意的实数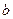 ,方程
,方程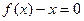 总有两个相异的实数根。...........1’
总有两个相异的实数根。...........1’
∴ 中
中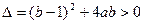 ,
,
即 恒成立。………………………....................2’
恒成立。………………………....................2’
故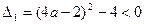 ,∴
,∴ 。………….........................2’
。………….........................2’
故当 时,对任意的实数
时,对任意的实数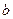 ,方程
,方程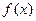 总有两个相异的不动点。 ………...................1’
总有两个相异的不动点。 ………...................1’
(3)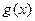 是R上的奇函数,则
是R上的奇函数,则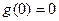 ,∴(0,0)是函数
,∴(0,0)是函数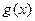 的不动点。 ……..................1’
的不动点。 ……..................1’
若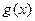 有异于(0,0)的不动点
有异于(0,0)的不动点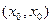 ,则
,则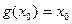 。
。
又 ,∴
,∴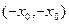 是函数
是函数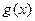 的不动点。
的不动点。
∴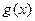 的有限个不动点除原点外,都是成对出现的, ..........................4’
的有限个不动点除原点外,都是成对出现的, ..........................4’
所以有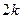 个(
个( ),加上原点,共有
),加上原点,共有 个。即
个。即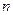 必为奇数
必为奇数
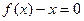 ,∴
,∴ …….1’
…….1’代入
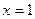 知
知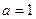 ,又由
,又由 及
及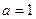 知
知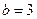 。……………………...2’
。……………………...2’∴
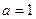 ,
,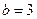 。 …………………………....................1’
。 …………………………....................1’(2)对任意实数
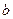 ,
,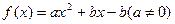 总有两个相异的不动点,即是对任意的实数
总有两个相异的不动点,即是对任意的实数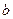 ,方程
,方程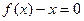 总有两个相异的实数根。...........1’
总有两个相异的实数根。...........1’∴
 中
中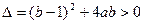 ,
,即
 恒成立。………………………....................2’
恒成立。………………………....................2’故
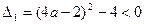 ,∴
,∴ 。………….........................2’
。………….........................2’故当
 时,对任意的实数
时,对任意的实数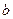 ,方程
,方程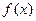 总有两个相异的不动点。 ………...................1’
总有两个相异的不动点。 ………...................1’(3)
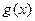 是R上的奇函数,则
是R上的奇函数,则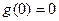 ,∴(0,0)是函数
,∴(0,0)是函数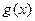 的不动点。 ……..................1’
的不动点。 ……..................1’若
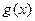 有异于(0,0)的不动点
有异于(0,0)的不动点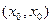 ,则
,则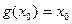 。
。又
 ,∴
,∴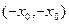 是函数
是函数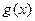 的不动点。
的不动点。∴
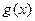 的有限个不动点除原点外,都是成对出现的, ..........................4’
的有限个不动点除原点外,都是成对出现的, ..........................4’所以有
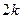 个(
个( ),加上原点,共有
),加上原点,共有 个。即
个。即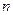 必为奇数
必为奇数 
练习册系列答案
相关题目
 ,
,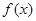 是定义在R上的且以2为周期的偶函数,当
是定义在R上的且以2为周期的偶函数,当 时,
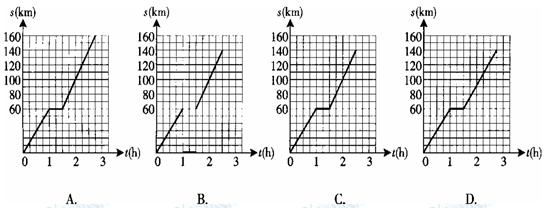
时, ,如果直线
,如果直线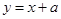 与曲线
与曲线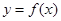 恰有两个不同的交点,则实数
恰有两个不同的交点,则实数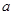 的值为 ( )
的值为 ( )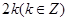
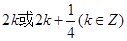
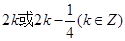
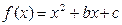 ,方程
,方程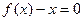 的两根为
的两根为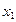 ,
,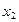 ,且
,且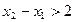
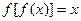 的另两个根为
的另两个根为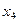 ,
,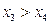 比较
比较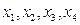 大小
大小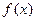 是(-
是(-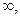 +
+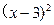 +4,求
+4,求
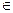 [1,2]时解析式
[1,2]时解析式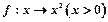 是集合A到集合B的映射,如果B=
是集合A到集合B的映射,如果B=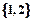 ,则
,则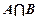 = .
= .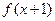 的定义域为
的定义域为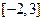 ,则
,则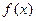 的定义域是( )
的定义域是( )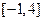
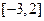
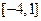
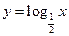 与函数
与函数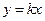 的图象有公共点
的图象有公共点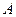 ,且点
,且点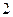 ,
,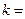 __________.
__________.