题目内容
某商店为了吸引顾客,设计了一个摸球小游戏,顾客从装有1个红球,1个白球,3个黑球的袋中一次随机的摸2个球,设计奖励方式如下表:
| 结果 | 奖励 |
| 1红1白 | 10元 |
| 1红1黑 | 5元 |
| 2黑 | 2元 |
| 1白1黑 | 不获奖 |
(1)某顾客在一次摸球中获得奖励X元,求X的概率分布表与数学期望;
(2)某顾客参与两次摸球,求他能中奖的概率.
解:(1)因为P(X=10)= =
= ,P(X=5)=
,P(X=5)= =
= ,
,
P(X=2)= =
= ,P(X=0) =
,P(X=0) = =
= ,
,
所以X的概率分布表为:
| X | 10 | 5 | 2 | 0 |
| P |
|
|
|
|
从而E(X)=10´ +5´
+5´ +2´
+2´ +0´
+0´ =3.1元.
=3.1元.
(2)记该顾客一次摸球中奖为事件A,由(1)知,P(A)= ,
,
从而他两次摸球中至少有一次中奖的概率P=1-[1-P(A)]2= .
.
答:他两次摸球中至少有一次中奖的概率为  .
.

练习册系列答案
相关题目
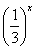 ,x∈[-1,1],函数
,x∈[-1,1],函数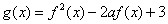 的最小
的最小 ,其中
,其中 。
。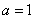 ,求函数
,求函数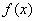 的极值点和极值;
的极值点和极值; 上的最小值。
上的最小值。
 上一点P引抛物线准线的垂线,
上一点P引抛物线准线的垂线,
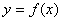 在(-∞,+∞)内有定义,对于给定的正数
在(-∞,+∞)内有定义,对于给定的正数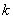 ,定义函数:
,定义函数: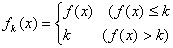 ,取函数
,取函数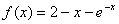 ,若对任意的
,若对任意的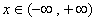 ,恒有
,恒有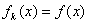 ,则
,则 B.
B. C.
C. D.
D.
 被
被 除所得的余数是_____________.
除所得的余数是_____________.