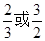题目内容
设圆锥曲线C的两个焦点分别为F1、F2,若曲线C上存在点P满足|PF1|∶|F1F2|∶|PF2|=4∶3∶2,则曲线C的离心率等于( )
(A) 或
或 (B)
(B) 或2
或2
(C) 或2 (D)
或2 (D) 或
或
【答案】
D
【解析】因为|PF1|∶|F1F2|∶|PF2|=4∶3∶2,
所以设|PF1|=4x,|F1F2|=3x,|PF2|=2x,x>0.
因为|F1F2|=3x=2c,
所以x= c.
c.
若曲线为椭圆,则有2a=|PF1|+|PF2|=6x,即a=3x,
所以离心率e= =
= =
= =
= .
.
若曲线为双曲线,则有2a=|PF1|-|PF2|=2x,即a=x,
所以离心率e= =
= =
= =
= .故选D.
.故选D.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
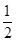 或
或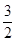 B.
B. 或2
C.
或2
C.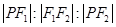
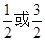 B.
B.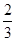 或2
或2 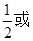 2
D.
2
D.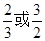
 =4:3:2,则曲线C的离心率等于( )
=4:3:2,则曲线C的离心率等于( )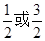 B.
B.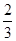 或2 C.
或2 C.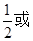 2
D.
2
D.