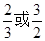题目内容
设圆锥曲线C的两个焦点分别为F1,F2,若曲线C上存在点P满足|PF1|:|F1F2|:|PF2|=6:5:4,则曲线C的离心率等于
或
或
.
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
分析:依题意,|PF1|:|F1F2|:|PF2|=6:5:4,可得|PF1|+|PF2|=2|F1F2|,再对圆锥曲线C是椭圆还是双曲线分类讨论,利用定义即可求得其离心率.
解答:解:∵|PF1|:|F1F2|:|PF2|=6:5:4,
∴|PF1|+|PF2|=2|F1F2|,
①若圆锥曲线C是椭圆,则2a=4c,
∴e=
=
;
②若圆锥曲线C是双曲线,
则e=
=
=
=
.
故答案为:
或
.
∴|PF1|+|PF2|=2|F1F2|,
①若圆锥曲线C是椭圆,则2a=4c,
∴e=
| c |
| a |
| 1 |
| 2 |
②若圆锥曲线C是双曲线,
则e=
| 2c |
| 2a |
| |F1F2| |
| |PF1|-|PF2| |
| 5 |
| 6-4 |
| 5 |
| 2 |
故答案为:
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查椭圆与双曲线的简单性质,由题意得到|PF1|+|PF2|=2|F1F2|是基础,对圆锥曲线C分类讨论是关键,考查分析问题、解决问题的能力,属于中档题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目



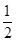 或
或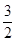 B.
B. 或2
C.
或2
C.
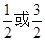 B.
B.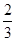 或2
或2 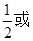 2
D.
2
D.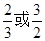
 =4:3:2,则曲线C的离心率等于( )
=4:3:2,则曲线C的离心率等于( )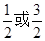 B.
B.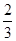 或2 C.
或2 C.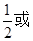 2
D.
2
D.