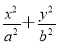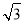题目内容
已知椭圆
＝1(a>b>0)的一个焦点为F，若椭圆上存在一个P点，满足以椭圆短轴为直径的圆与线段PF相切于该线段的中点，则该椭圆的离心率为( )．
A. 
B. 
C. 
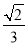D.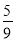 
A
【解析】不妨设F(－c,0)为椭圆的左焦点，F1为椭圆的右焦点．P点在椭圆上，线段PF的中点为M，则|PM|＝|FM|，圆x2＋y2＝b2与线段PF相切于点M，则|MO|＝b(O为坐标原点)．显然有OM为△FPF1的中位线，则|PF1|＝2|OM|＝2b.由勾股定理可得|PF|＝2|FM|＝2
.再由椭圆定义可知，|PF|＋|PF1|＝2a，所以2
＋2b＝2a，所以c2－b2＝(a－b)2＝a2－2ab＋b2，结合a2－c2＝b2得2ab＝3b2.所以2a＝3b，所以e＝
＝
＝
.
练习册系列答案
名师金手指领衔课时系列答案
相关题目
