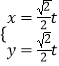题目内容
【题目】函数f（x）=x|x|．若存在x∈[1，+∞），使得f（x﹣2k）﹣k＜0，则k的取值范围是（ ）
A.（2，+∞）
B.（1，+∞）
C.（ 
，+∞）
D.（ 
，+∞）
【答案】D
【解析】解：根据题意，x∈[1，+∞）时，x﹣2k∈[1﹣2k，+∞）；
①当1﹣2k≤0时，解得k≥ 
；存在x∈[1，+∞），使得f（x﹣2k）﹣k＜0，
即只要f（1﹣2k）﹣k＜0即可；
∵1﹣2k≤0，∴f（1﹣2k）=﹣（1﹣2k）2，
∴﹣（1﹣2k）2﹣k＜0，整理得﹣1+4k﹣4k2﹣k＜0，即4k2﹣3k+1＞0；
∵△=（﹣3）2﹣16=﹣7＜0，
∴不等式对一切实数都成立，∴k≥ ；
②当1﹣2k＞0时，解得k＜ ；
存在x∈[1，+∞），使得f（x﹣2k）﹣k＜0，
即只要f（1﹣2k）﹣k＜0即可；
∵1﹣2k＞0，∴f（1﹣2k）=（1﹣2k）2，
∴（1﹣2k）2﹣k＜0，整理得4k2﹣5k+1＜0，解得 
＜k＜1；
又∵k＜ ，∴ ＜k＜ ；
综上，k∈（ ， ）∪[ ，+∞）=（ +∞）；
∴k的取值范围是k∈（ ，+∞）．
故选：D．
【考点精析】解答此题的关键在于理解特称命题的相关知识，掌握特称命题
：
，
，它的否定
：
，
;特称命题的否定是全称命题．
练习册系列答案
相关题目
