题目内容
【题目】设![]() ,
, ![]() .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)讨论![]() 在区间
在区间![]() 上的极值点个数;
上的极值点个数;
(3)是否存在![]() ,使得
,使得![]() 在区间
在区间![]() 上与
上与![]() 轴相切?若存在,求出所有
轴相切?若存在,求出所有![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)减区间为![]() ,增区间为
,增区间为![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】试题分析:(1)先求函数![]() 导数,再求导函数零点,列表分析导函数符号变化规律,确定单调区间(2)先求函数
导数,再求导函数零点,列表分析导函数符号变化规律,确定单调区间(2)先求函数![]() 导数,转化为研究
导数,转化为研究![]() 零点个数,利用二次求导易得
零点个数,利用二次求导易得![]() 在区间
在区间![]() 上单调递增,其零点个数决定于最小值的大小,讨论其最小值与零的大小得到极值点个数, (3)由题意得
上单调递增,其零点个数决定于最小值的大小,讨论其最小值与零的大小得到极值点个数, (3)由题意得![]() 在区间
在区间![]() 上与
上与![]() 轴相切切点为极值点
轴相切切点为极值点![]() ,由(2)得
,由(2)得![]() ,再根据极值点定义可得方程组
,再根据极值点定义可得方程组![]() ,解得
,解得![]()
试题解析:解:(1)当![]() 时:
时:![]() ,(
,(![]() )
)
故![]()
![]()
当![]() 时:
时:![]() ,当
,当![]() 时:
时:![]() ,当
,当![]() 时:
时:![]() .
.
故![]() 的减区间为:
的减区间为:![]() ,增区间为
,增区间为![]()
(2)![]()
令![]()
![]() ,故
,故![]() ,
,![]() ,
,
显然![]() ,又当
,又当![]() 时:
时:![]() .当
.当![]() 时:
时:![]() .
.
故![]()
![]() ,
,![]()
![]() ,
,![]() .
.
故![]() 在区间
在区间![]() 上单调递增,
上单调递增,
注意到:当![]() 时,
时,![]()
![]() ,故
,故![]() 在
在![]() 上的零点个数由
上的零点个数由![]() 的符号决定.
的符号决定.
①当![]() ,即:
,即:![]() 或
或![]() 时:
时:![]() 在区间
在区间![]() 上无零点,即
上无零点,即![]() 无极值点.
无极值点.
②当![]() ,即:
,即:![]() 时:
时:![]() 在区间
在区间![]() 上有唯一零点,即
上有唯一零点,即![]() 有唯一极值点.
有唯一极值点.
综上:当![]() 或
或![]() 时:
时:![]() 在
在![]() 上无极值点.
上无极值点.
当![]() 时:
时:![]() 在
在![]() 上有唯一极值点.
上有唯一极值点.
(3)假设存在![]() ,使得
,使得![]() 在区间
在区间![]() 上与
上与![]() 轴相切,则
轴相切,则![]() 必与
必与![]() 轴相切于极值点处,
轴相切于极值点处,
由(2)可知:![]() .不妨设极值点为
.不妨设极值点为![]() ,则有:
,则有:
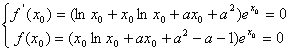 …(*)同时成立.
…(*)同时成立.
联立得:![]() ,即
,即![]() 代入(*)可得
代入(*)可得![]() .
.
令![]() ,
,![]() .
.
则![]() ,
,![]() ,当
,当 ![]() 时
时![]() (
(![]()
![]()
![]() 2).
2).
故![]() 在
在![]() 上单调递减.又
上单调递减.又![]() ,
, ![]() .
.
故![]() 在
在![]() 上存在唯一零点
上存在唯一零点![]() .
.
即当![]() 时
时![]() ,
,![]() 单调递增.当
单调递增.当![]() 时
时![]() ,
,![]() 单调递减.
单调递减.
因为![]() ,
,![]() .
.
故![]() 在
在![]() 上无零点,在
上无零点,在![]() 上有唯一零点.
上有唯一零点.
由观察易得![]() ,故
,故![]() ,即:
,即:![]() .
.
综上可得:存在唯一的![]() 使得
使得![]() 在区间
在区间![]() 上与
上与![]() 轴相切.
轴相切.

【题目】“累积净化量![]() ”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据
”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据![]() 《空气净化器》国家标准,对空气净化器的累计净化量
《空气净化器》国家标准,对空气净化器的累计净化量![]() 有如下等级划分:
有如下等级划分:
累积净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器(共5000台)的质量,随机抽取![]() 台机器作为样本进行估计,已知这
台机器作为样本进行估计,已知这![]() 台机器的累积净化量都分布在区间
台机器的累积净化量都分布在区间![]() 中,按照
中,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均匀分组,其中累积净化量在
均匀分组,其中累积净化量在![]() 的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
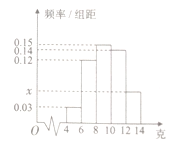
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共5000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累积净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.