题目内容
已知数列{an}中,a1=1,an+1=c-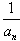 。
。
(1)设c=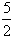 ,bn=
,bn=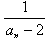 ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(2)求使不等式an<an+1<3成立的c的取值范围。
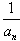 。
。(1)设c=
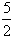 ,bn=
,bn=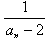 ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;(2)求使不等式an<an+1<3成立的c的取值范围。
解:(1)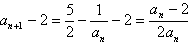
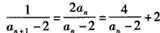 ,即
,即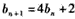
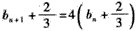 又
又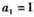 ,故
,故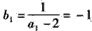
所以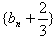 是首项为
是首项为 ,公比为4的等比数列
,公比为4的等比数列
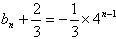 ,
,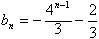 ;
;
(2)a1=1,a2=c-1,由a2>a1得c>2
用数学归纳法证明:当c>2时,an<an+1
(i)当n=1时,a2=c-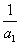 >a1,命题成立;
>a1,命题成立;
(ii)设当n=k时,ak<ak+1,则当n=k+1时
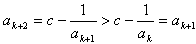
故由(i)(ii)知当c>2时,an<an+1
当c>2时,令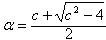
由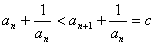 得an<α
得an<α
当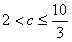 时,an<α≤3
时,an<α≤3
当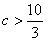 时,α>3,且1≤an<a,于是
时,α>3,且1≤an<a,于是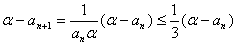
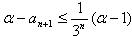
当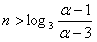 时,α-an+1<α-3,an+1>3
时,α-an+1<α-3,an+1>3
因此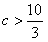 不符合要求
不符合要求
所以c的取值范围是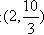 。
。
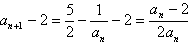
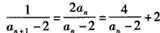 ,即
,即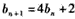
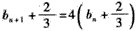 又
又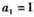 ,故
,故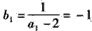
所以
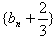 是首项为
是首项为 ,公比为4的等比数列
,公比为4的等比数列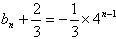 ,
,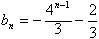 ;
;(2)a1=1,a2=c-1,由a2>a1得c>2
用数学归纳法证明:当c>2时,an<an+1
(i)当n=1时,a2=c-
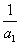 >a1,命题成立;
>a1,命题成立;(ii)设当n=k时,ak<ak+1,则当n=k+1时
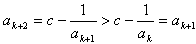
故由(i)(ii)知当c>2时,an<an+1
当c>2时,令
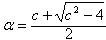
由
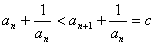 得an<α
得an<α当
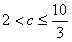 时,an<α≤3
时,an<α≤3当
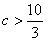 时,α>3,且1≤an<a,于是
时,α>3,且1≤an<a,于是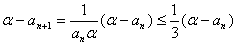
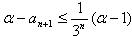
当
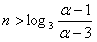 时,α-an+1<α-3,an+1>3
时,α-an+1<α-3,an+1>3因此
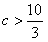 不符合要求
不符合要求所以c的取值范围是
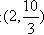 。
。
练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|