题目内容
求函数 的极值
的极值
,当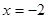 时,
时,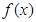 有极大值且极大值为
有极大值且极大值为 ;
;
当 时,
时,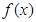 有极小值且极小值为
有极小值且极小值为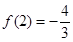
解析试题分析:
求函数的极值,首先找到定义域使得函数有意义,其次求导函数,令其等于零,分析函数的单调性,从而找到极值点,求出极值.
试题解析:
根据题意可知函数定义域为 ,
,
因为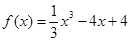 ,所以
,所以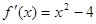 ,令
,令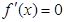 ,可得
,可得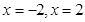 ,
,
当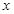 变化时,有下表
变化时,有下表 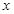

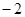
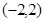
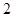
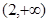

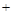
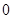
- 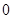
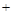
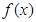
↗ 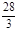
↘ 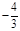
↗
由上表可知,当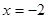 时,
时,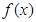 有极大值且极大值为
有极大值且极大值为 ;
;
当 时,
时,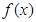 有极小值且极小值为
有极小值且极小值为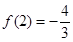
考点:导数法求极值.

练习册系列答案
相关题目
题目内容
求函数 的极值
的极值
,当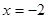 时,
时,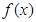 有极大值且极大值为
有极大值且极大值为 ;
;
当 时,
时,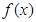 有极小值且极小值为
有极小值且极小值为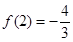
解析试题分析:
求函数的极值,首先找到定义域使得函数有意义,其次求导函数,令其等于零,分析函数的单调性,从而找到极值点,求出极值.
试题解析:
根据题意可知函数定义域为 ,
,
因为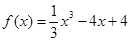 ,所以
,所以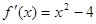 ,令
,令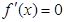 ,可得
,可得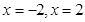 ,
,
当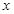 变化时,有下表
变化时,有下表 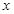

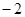
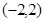
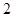
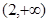

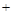
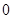
- 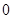
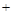
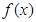
↗ 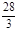
↘ 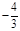
↗
由上表可知,当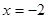 时,
时,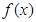 有极大值且极大值为
有极大值且极大值为 ;
;
当 时,
时,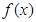 有极小值且极小值为
有极小值且极小值为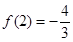
考点:导数法求极值.
