Question

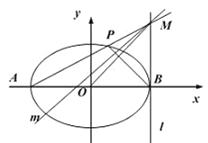
【题目】如图，在平面直角坐标系中，椭圆的焦距为2，且过点.

（1）求椭圆的方程；

（2）若点分别是椭圆的左右顶点，直线经过点且垂直与轴，点是椭圆上异于的任意一点，直线交于点.

①设直线的斜率为，直线的斜率为，求证：为定值；

②设过点垂直于的直线为 ，求证：直线过定点，并求出定点的坐标.

Answer 1

【答案】（1）；（2），.

【解析】试题分析：（1）根据条件列方程组，解得，（2）①设，则可由直线交点得，再根据斜率公式化简，最后利用点P在椭圆上得定值；②先探求定点为，再根据点斜式写出直线方程，最后令y=0解得x=-1.

试题解析：（1）由题意椭圆的焦距为2，且过点，

所以，解得，

所以椭圆的标准方程为.

（2）①设，则直线的方程为，

令得，因为，因为，

所以，因为在椭圆上，所以，

所以为定值，

②直线的斜率为，直线的斜率为，

则直线的方程为，

所以直线过定点.