题目内容
若函数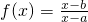 在区间(-∞,4)上是增函数,则有
在区间(-∞,4)上是增函数,则有
- A.a>b≥4
- B.a≥4>b
- C.4≤a<b
- D.a≤4<b
C
分析:求导函数,利用导数大于0,求得a<b,确定函数的单调增区间,根据函数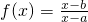 在区间(-∞,4)上是增函数,即可求得结论.
在区间(-∞,4)上是增函数,即可求得结论.
解答:求导函数可得 =
=
令f′(x)>0,可得b-a>0,∴a<b
∵函数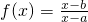 的单调区间为(-∞,a),(a,+∞),函数
的单调区间为(-∞,a),(a,+∞),函数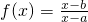 在区间(-∞,4)上是增函数
在区间(-∞,4)上是增函数
∴a≥4
∴4≤a<b
故选C.
点评:本题考查函数的单调性,考查导数知识的运用,正确理解函数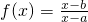 在区间(-∞,4)上是增函数是关键.
在区间(-∞,4)上是增函数是关键.
分析:求导函数,利用导数大于0,求得a<b,确定函数的单调增区间,根据函数
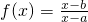 在区间(-∞,4)上是增函数,即可求得结论.
在区间(-∞,4)上是增函数,即可求得结论.解答:求导函数可得
 =
=
令f′(x)>0,可得b-a>0,∴a<b
∵函数
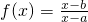 的单调区间为(-∞,a),(a,+∞),函数
的单调区间为(-∞,a),(a,+∞),函数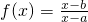 在区间(-∞,4)上是增函数
在区间(-∞,4)上是增函数∴a≥4
∴4≤a<b
故选C.
点评:本题考查函数的单调性,考查导数知识的运用,正确理解函数
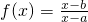 在区间(-∞,4)上是增函数是关键.
在区间(-∞,4)上是增函数是关键. 
练习册系列答案
相关题目
