题目内容
已知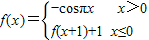 ,则f(
,则f( )+f(-
)+f(- )的值等于 .
)的值等于 .
【答案】分析:根据 ,-
,- 与分段点0进行比较,代入相应的解析式,然后根据特殊值的三角函数进行求值即可.
与分段点0进行比较,代入相应的解析式,然后根据特殊值的三角函数进行求值即可.
解答:解:∵ >0,当x>0时,f(x)=-cosπx
>0,当x>0时,f(x)=-cosπx
∴f( )=-cos
)=-cos π=
π=
∵- <0,当x≤0时,f(x)=f(x+1)+1
<0,当x≤0时,f(x)=f(x+1)+1
∴f(- )=f(
)=f( )+1=1-cos
)+1=1-cos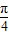 =1-
=1-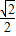
∴f( )+f(-
)+f(- )=
)= +1-
+1-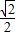 =
=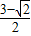
故答案为: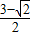
点评:本题主要考查了分段函数求值,以及三角函数求值,同时考查了运算求解的能力,属于基础题.
 ,-
,- 与分段点0进行比较,代入相应的解析式,然后根据特殊值的三角函数进行求值即可.
与分段点0进行比较,代入相应的解析式,然后根据特殊值的三角函数进行求值即可.解答:解:∵
 >0,当x>0时,f(x)=-cosπx
>0,当x>0时,f(x)=-cosπx∴f(
 )=-cos
)=-cos π=
π=
∵-
 <0,当x≤0时,f(x)=f(x+1)+1
<0,当x≤0时,f(x)=f(x+1)+1∴f(-
 )=f(
)=f( )+1=1-cos
)+1=1-cos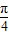 =1-
=1-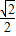
∴f(
 )+f(-
)+f(- )=
)= +1-
+1-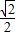 =
=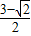
故答案为:
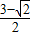
点评:本题主要考查了分段函数求值,以及三角函数求值,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
已知函数y=f(x)的定义域为(0,+∞),f(x)的导函数为f′(x),且对任意正数X均有f′(x)>
,则下列结论中正确的是( )
| f(x) |
| x |
| A、y=f(x)在(0,+∞)上为增函数 | ||
B、y=
| ||
| C、若x1,x2∈(0,+∞)则f((x1)+f(x2)>f(x1+x2) | ||
| D、若x1,x2∈(0,+∞),则f(x1)+f(x2)<f(x1+x2) |