题目内容
设锐角△ABC的三内角A,B,C,向量
=(sinA+
cosA,-1),
=(sinA,
),且
⊥
则角A的大小为
.
| m |
| 3 |
| n |
| 3 |
| 2 |
| m |
| n |
| π |
| 3 |
| π |
| 3 |
分析:由向量
=(sinA+
cosA,-1),
=(sinA,
),且
⊥
,知sinA(sinA+
cosA)-
=0,整理,得
sin2A-
cos2A=sin(2A-
)=1,由锐角△ABC的三内角A,B,C,能求出角A.
| m |
| 3 |
| n |
| 3 |
| 2 |
| m |
| n |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
解答:解:∵向量
=(sinA+
cosA,-1),
=(sinA,
),且
⊥
,
∴sinA(sinA+
cosA)-
=0,
∴sin2A+
sinAcosA=
,
∴
+
sin2A=
,
整理,得
sin2A-
cos2A=sin(2A-
)=1,
∵锐角△ABC的三内角A,B,C,
∴2A-
=
,
∴A=
.
故答案为:
.
| m |
| 3 |
| n |
| 3 |
| 2 |
| m |
| n |
∴sinA(sinA+
| 3 |
| 3 |
| 2 |
∴sin2A+
| 3 |
| 3 |
| 2 |
∴
| 1-cos2A |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
整理,得
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∵锐角△ABC的三内角A,B,C,
∴2A-
| π |
| 6 |
| π |
| 2 |
∴A=
| π |
| 3 |
故答案为:
| π |
| 3 |
点评:本题考查向量的应用,解题时要认真审题,注意三角函数恒等式的合理运用.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 且
且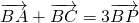 则下列正确的命题序号是________.
则下列正确的命题序号是________. 且
且 则下列正确的命题序号是 .
则下列正确的命题序号是 .