题目内容
如图,已知平面四边形ABCD中,D为PA的中点,PA⊥AB,CD∥AB,且PA=CD=2AB=4,将此平面四边形ABCD沿CD折成直二面角P-DC-B,连接PA、PB,设PB的中点为E,
(Ⅰ)求证:平面PBD⊥平面PBC;
(Ⅱ)求直线AB与平面PBC所成角的正弦值;
(Ⅲ)在线段BD上是否存在一点F,使得EF⊥平面PBC?若存在,请确定点F的位置;若不存在,请说明理由.

(Ⅰ)求证:平面PBD⊥平面PBC;
(Ⅱ)求直线AB与平面PBC所成角的正弦值;
(Ⅲ)在线段BD上是否存在一点F,使得EF⊥平面PBC?若存在,请确定点F的位置;若不存在,请说明理由.

考点:直线与平面所成的角,直线与平面垂直的性质,平面与平面垂直的判定
专题:空间角
分析:(Ⅰ)根据面面垂直的判定定理即可证明平面PBD⊥平面PBC;
(Ⅱ)建立空间坐标系,利用向量法即可求出直线AB与平面PBC所成角的正弦值;
(Ⅲ)利用向量法,结合EF⊥平面PBC的判定定理即可求出点F的位置;
(Ⅱ)建立空间坐标系,利用向量法即可求出直线AB与平面PBC所成角的正弦值;
(Ⅲ)利用向量法,结合EF⊥平面PBC的判定定理即可求出点F的位置;
解答:
(I)证明:直二面角P-DC-B的平面角为∠PDA=90°,且PD⊥DC,DA∩DC=D,
∴PD⊥平面ABCD,
∵BC?平面ABCD,∴PD⊥BC,
则BC=BD=
=2
,
在三角形BCD中,BC2+BD2=CD2,
∴BD⊥BC,
∵PD∩BD=D,∴BC⊥平面PBD,
∵BC?平面PBC,
∴平面PBD⊥平面PBC.
(II)∵PD,PA,DC两两垂直,PA=CD=2AB=4,
∴AB=2,∵E是PB的中点,
∴AD=DP=2,
则建立以D为原点的空间直角坐标系如图,
则A(2,0,0),B(2,2,0),C(0,4,0),D(0,0,0),P(0,0,2),
则
=(0,2,0),
=(-2,2,0),
=(0,4,-2).
设平面PBC的法向量为
=(x,y,z),
则由
,令x=1,则y=1,z=2,即
=(1,1,2),
则cos<
,
>=
=
=
,
∴直线AB和平面PBC所成角的正弦值等于cos<
,
>=
,
(III)∵F∈BD,故可设F(m,m,0),而PB的中点E(1,1,1),
∴
=(m-1,m-1,-1),
∵
•
=0,
•
=0,
∴
,解得m=
,
∴线段BD上是否存在一点F(
,
,0),使EF⊥平面PBC.
∴PD⊥平面ABCD,

∵BC?平面ABCD,∴PD⊥BC,
则BC=BD=
| AB2+AD2 |
| 2 |
在三角形BCD中,BC2+BD2=CD2,
∴BD⊥BC,
∵PD∩BD=D,∴BC⊥平面PBD,
∵BC?平面PBC,
∴平面PBD⊥平面PBC.
(II)∵PD,PA,DC两两垂直,PA=CD=2AB=4,
∴AB=2,∵E是PB的中点,
∴AD=DP=2,
则建立以D为原点的空间直角坐标系如图,
则A(2,0,0),B(2,2,0),C(0,4,0),D(0,0,0),P(0,0,2),
则
| AB |
| BC |
| PC |
设平面PBC的法向量为
| n |
则由
|
| n |
则cos<
| AB |
| n |
| ||||
|
|
| 2 | ||
2×
|
| ||
| 6 |
∴直线AB和平面PBC所成角的正弦值等于cos<
| AB |
| n |
| ||
| 6 |
(III)∵F∈BD,故可设F(m,m,0),而PB的中点E(1,1,1),
∴
| EF |
∵
| EF |
| BC |
| EF |
| PC |
∴
|
| 1 |
| 2 |
∴线段BD上是否存在一点F(
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查空间面面垂直的判断,以及线面垂直,线面角的求解,要求熟练掌握相应的判定定理以及利用空间向量法是解决本题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
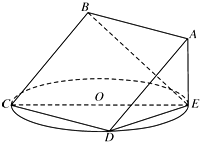 如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点.
如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点.