题目内容
(本题满分14分)
已知在平面直角坐标系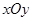 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为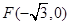 ,右顶点为
,右顶点为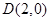 ,设点
,设点 .
.
(1)求该椭圆的标准方程;
(2)若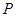 是椭圆上的动点,求线段
是椭圆上的动点,求线段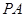 中点
中点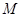 的轨迹方程;
的轨迹方程;
(3)过原点 的直线交椭圆于点
的直线交椭圆于点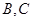 ,求
,求 面积的最大值。
面积的最大值。
(1)(2) (3)
(3)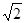
解析试题分析:解:(1)由已知得椭圆的半长轴a=2,半焦距c= ,则半短轴b=1.
,则半短轴b=1.
又椭圆的焦点在x轴上, ∴椭圆的标准方程为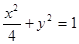
(2)设线段PA的中点为M(x,y) ,点P的坐标是(x0,y0),
由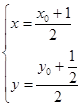 得
得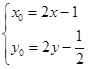
又点P在椭圆上,得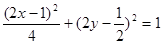 ,
,
∴线段PA中点M的轨迹方程是 .
.
(3)当直线BC垂直于x轴时,BC=2,因此△ABC的面积S△ABC=1.
当直线BC不垂直于x轴时,设该直线方程为y=kx,代入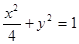 ,
,
解得B(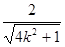 ,
,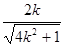 ),C(-
),C(-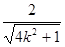 ,-
,-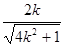 ),
),
则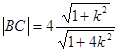 ,又点A到直线BC的距离d=
,又点A到直线BC的距离d=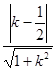 ,
,
∴△ABC的面积S△ABC=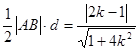
于是S△ABC=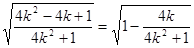
由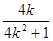 ≥-1,得S△ABC≤
≥-1,得S△ABC≤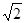 ,其中,当k=-
,其中,当k=- 时,等号成立.
时,等号成立.
∴S△ABC的最大值是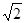 .
.
考点:椭圆的方程以及直线与椭圆的位置关系
点评:解决的关键是利用椭圆的性质得到a,b,c的关系式,同时联立方程组,结合韦达定理来表示轨迹方程,结合距离公式得到面积,属于基础题。

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
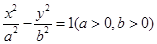 与椭圆
与椭圆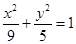 有相同的焦点
有相同的焦点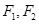 ,且该双曲线
,且该双曲线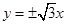 .
.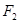 作斜率不为零的直线与此双曲线的左,右两支分别交于点
作斜率不为零的直线与此双曲线的左,右两支分别交于点 、
、 ,
,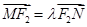 ,当
,当 轴上的点
轴上的点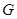 满足
满足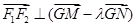 时,求点
时,求点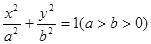 ,左焦点
,左焦点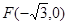 ,且离心率
,且离心率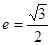
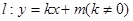 与椭圆C交于不同的两点
与椭圆C交于不同的两点 (
( 为直径的圆经过椭圆C的右顶点A. 求证:直线
为直径的圆经过椭圆C的右顶点A. 求证:直线 过定点,并求出定点的坐标.
过定点,并求出定点的坐标. 的方程为
的方程为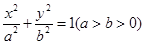 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b). ,求点
,求点 的坐标;
的坐标;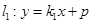 交椭圆
交椭圆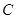 、
、 两点,交直线
两点,交直线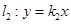 于点
于点 .若
.若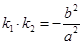 ,证明:
,证明: 的中点;
的中点;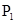 、
、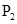 满足
满足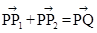 ,写出求作点
,写出求作点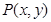 到直线
到直线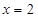 的距离与它到定点
的距离与它到定点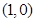 的距离之比为
的距离之比为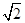 ,并记点
,并记点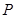 的轨迹为曲线
的轨迹为曲线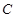 .
.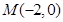 ,过点
,过点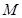 的直线
的直线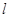 与曲线
与曲线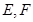 两点,当线段
两点,当线段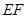 的中点落在由四点
的中点落在由四点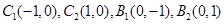 构成的四边形内(包括边界)时,求直线
构成的四边形内(包括边界)时,求直线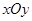 中,以O为极点,
中,以O为极点,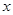 轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为
轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为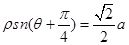 ,曲线
,曲线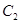 的参数方程为
的参数方程为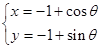 ,(
,(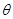 为参数,
为参数,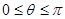 )。
)。 的取值范围。
的取值范围。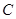 :
: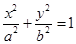 (
(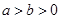 )的离心率为
)的离心率为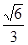 ,过右焦点
,过右焦点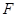 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆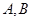 两点,
两点,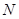 为弦
为弦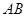 的中点。
的中点。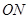 (
( 为坐标原点)的斜率
为坐标原点)的斜率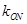 ;
;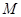 椭圆
椭圆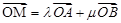 ,求
,求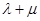 的最大值和最小值.
的最大值和最小值.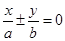 称为椭圆
称为椭圆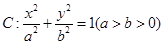 的“特征直线”,若椭圆的离心率
的“特征直线”,若椭圆的离心率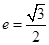 .(1)求椭圆的“特征直线”方程;
.(1)求椭圆的“特征直线”方程;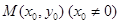 作圆
作圆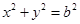 的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若
的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若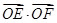 取值范围恰为
取值范围恰为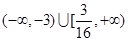 ,求椭圆C的方程.
,求椭圆C的方程.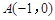 ,
,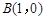 ,△
,△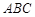 的周长为6.
的周长为6. 的轨迹
的轨迹 的方程;
的方程; 与曲线
与曲线 ,
, .若点
.若点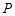 在
在 轴上,且
轴上,且 ,求点
,求点