题目内容
16．过抛物线y2=2px（p＞0）的焦点F的直线交抛物线于A，B两点．点O是原点，如果|BF|=3，|BF|＞|AF|，∠BFO=$\frac{2π}{3}$，那么|AF|的值为1．分析 如图，作BN⊥准线l，AM⊥l，AC⊥BN，利用抛物线的定义，及|∠BFO=$\frac{2π}{3}$，即可求出|AF|的值．
解答 
解：如图，作BN⊥准线l，AM⊥l，AC⊥BN，
∴|BF|=|BN|，|AF|=|AM|，
∵∠BFO=$\frac{2π}{3}$，∴cos∠BCF=$\frac{1}{2}$=$\frac{|BF|-|AF|}{|BF|+|AF|}$，
∵|BF|=3，
∴|AF|=1，
故答案为：1．
点评 本题考查抛物线的定义，考查特殊角的三角函数，正确转化是关键．
练习册系列答案
相关题目
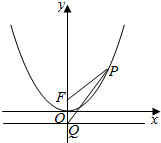如图，设抛物线x2=4y的焦点为F，其准线与y轴相交于点Q，设P为抛物线上的一点，若$|{PQ}|=\sqrt{2}|{PF}|$，则△PQF的面积为2．