题目内容
已知函数f(x)=x2+bx+c,且f(1)=0,f(3)=0,则c-b+1= .
【答案】分析:将f(1)=0,f(3)=0分别代入二次函数的解析式,列出关于b、c的方程组,通过解方程组求得b、c的值;然后将其代入所求式即可.
解答:解:根据题意,
得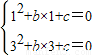 ,
,
解得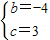
则c-b+1=8.
故答案为 8
点评:本题考查了待定系数法求二次函数的解析式.一般用法是,设某一多项式的全部或部分系数为未知数,利用两个多项式恒等时同类项系数相等的原理或其他已知条件确定这些系数,从而得到待求的值.
解答:解:根据题意,
得
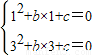 ,
,解得
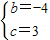
则c-b+1=8.
故答案为 8
点评:本题考查了待定系数法求二次函数的解析式.一般用法是,设某一多项式的全部或部分系数为未知数,利用两个多项式恒等时同类项系数相等的原理或其他已知条件确定这些系数,从而得到待求的值.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|