题目内容
已知f(x)=sin(2x+
)
（1）求函数f（x）的递减区间；
（2）用五点法作出函数在一个周期内的图象，并说明它是由y=sinx的图象依次经过哪些变换而得到的？
| π | 3 |
（1）求函数f（x）的递减区间；
（2）用五点法作出函数在一个周期内的图象，并说明它是由y=sinx的图象依次经过哪些变换而得到的？
分析：（1）根据正弦函数单调区间的公式解关于x的不等式，即可得到函数f（x）的递减区间；
（2）分别令2x+
=0、
、π、
、2π，可得x=-
、
、
、
、
，由此得到函数在一个周期内图象上的关键的点，描出这五个点的坐标再连成平滑的曲线，即可得到函数在一个周期内的图象．最后由函数图象平移、伸缩的公式加以计算，可得由y=sinx的图象变换到f(x)=sin(2x+
)的方法．
（2）分别令2x+
| π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 6 |
| π |
| 12 |
| π |
| 3 |
| 7π |
| 12 |
| 5π |
| 6 |
| π |
| 3 |
解答：解：（1）对于函数f(x)=sin(2x+
)，
令
+2kπ≤2x+
≤
+2kπ（k∈Z），得
+kπ≤x≤
+kπ（k∈Z），
∴函数f（x）的递减区间为[
+kπ，
+kπ]，（k∈Z）．
（2）列出如下表格：
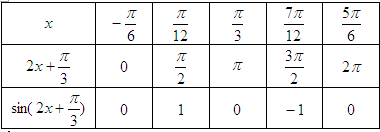
在直角坐标系中描出点（-
，0），（
，1），（
，0），（
，-1），（
，0）．
连成平滑的曲线如图所示，即为函数f(x)=sin(2x+
)在一个周期内的图象，
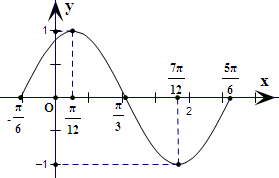
将y=sinx的图象先向左平移
个单位，再将所得图象上点的纵坐标不变，
横坐标变为原来的一半，可得函数f(x)=sin(2x+
)的图象．
| π |
| 3 |
令
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 12 |
| 7π |
| 12 |
∴函数f（x）的递减区间为[
| π |
| 12 |
| 7π |
| 12 |
（2）列出如下表格：
在直角坐标系中描出点（-
| π |
| 6 |
| π |
| 12 |
| π |
| 3 |
| 7π |
| 12 |
| 5π |
| 6 |
连成平滑的曲线如图所示，即为函数f(x)=sin(2x+
| π |
| 3 |
将y=sinx的图象先向左平移
| π |
| 3 |
横坐标变为原来的一半，可得函数f(x)=sin(2x+
| π |
| 3 |
点评：本题给出正弦型三角函数，求它的单调区间并作出一个周期内的图象，着重考查了三角函数的单调性、三角函数的图象作法与函数图象的变换公式等知识，属于中档题．
练习册系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
相关题目
已知f(x)=sin(2x-
)-2m在x∈[0，
]上有两个零点，则m的取值范围为（ ）
| π |
| 6 |
| π |
| 2 |
A、(
| ||||
B、[
| ||||
C、[
| ||||
D、（
|
已知f(x)=sin(x+
)，g(x)=cos(x-
)，则下列结论中正确的是（ ）
| π |
| 2 |
| π |
| 2 |
| A、函数y=f（x）•g（x）的周期为2 | ||
| B、函数y=f（x）•g（x）的最大值为1 | ||
C、将f（x）的图象向左平移
| ||
D、将f（x）的图象向右平移
|