题目内容
设A={(x,y)|y2－x－1=0},B={(x,y)|4x2+2x－2y+5=0},C={(x,y)|y=kx+b},是否存在k、b∈N,使得(A∪B)∩C=
，证明此结论.
k=1,故存在自然数k=1,b=2,使得(A∪B)∩C=
解析:
∵(A∪B)∩C=，∴A∩C=且B∩C=
∵
∴k2x2+(2bk－1)x+b2－1=0
∵A∩C=
∴Δ1=(2bk－1)2－4k2(b2－1)<0
∴4k2－4bk+1<0,此不等式有解，
其充要条件是16b2－16>0,
即 b2>1 ①
∵
∴4x2+(2－2k)x+(5+2b)=0
∵B∩C=,∴Δ2=(1－k)2－4(5－2b)<0
∴k2－2k+8b－19<0, 从而8b<20,
即 b<2.5 ②
由①②及b∈N,得b=2代入由Δ1<0和Δ2<0组成的不等式组，得
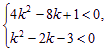
∴k=1,故存在自然数k=1,b=2,使得(A∪B)∩C=.
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
设A={x|y=ln(2+x-x2)，x∈R}，B={y|y=
，x∈A}，则CAB=（ ）
| x+2 |
| A、（-∞，-1]∪[2，+∞） |
| B、（-1，0） |
| C、（-∞，0]∪[2，+∞） |
| D、（-1，1] |