题目内容
已知正实数x,y,设a=x+y,b=
.
(1)当y=1时,求
的取值范围;
(2)若以a,b为三角形的两边,第三条边长为c构成三角形,求
的取值范围.
| x2+7xy+y2 |
(1)当y=1时,求
| b |
| a |
(2)若以a,b为三角形的两边,第三条边长为c构成三角形,求
| c2 |
| xy |
分析:(1)法一:当y=1时,x=a-1,由x,y均为正实数,代入b=
,可得
=
,进而根据二次函数的图象和性质得到
的取值范围;
法二:当y=1时,根据a=x+y,b=
,可将
化为
的形式,进而利用基本不等式求出
的取值范围;
(2)
=k,则c=
,由于a,b,c为三角形的三边,由“任意两边之和大于第三边,任意两边之差小于第三边”构造关于k的不等式组,进而根据对勾函数的单调性,求出
的取值范围.
| x2+7xy+y2 |
| b |
| a |
-5(
|
| b |
| a |
法二:当y=1时,根据a=x+y,b=
| x2+7xy+y2 |
| b |
| a |
1+
|
| b |
| a |
(2)
| c2 |
| xy |
| k•xy |
| c2 |
| xy |
解答:解:(1)由题设知,x=a-1,且a=x+1>1
所以,
=
=
=
又a=x+1>1⇒
∈(0,1)
结合二次函数的图象知1<-5(
-
)2+
≤
故
的取值范围为(1,
]
另解:
=
=
=
=
,∵x+2+
≥4,0<
≤
∴1<
≤
,得
的取值范围为(1,
]
(2)设
=k,则c=
∵
恒成立,
即
,恒成立
令
=t,由于y=t+
在[1,+∞)是增函数,令f(t)=
+
,则f(t)=
+
≥
+
=5
又∵
-
=
≤1∴1<
<5,1<k<25,
得
的取值范围为(1,25)
所以,
| b |
| a |
| ||
| a |
|
-5(
|
又a=x+1>1⇒
| 1 |
| a |
结合二次函数的图象知1<-5(
| 1 |
| a |
| 1 |
| 2 |
| 9 |
| 4 |
| 9 |
| 4 |
故
| b |
| a |
| 3 |
| 2 |
另解:
| b |
| a |
| ||
| x+1 |
|
1+
|
=
1+
|
| 1 |
| x |
| 5 | ||
x+2+
|
| 5 |
| 4 |
| b |
| a |
| 3 |
| 2 |
| b |
| a |
| 3 |
| 2 |
(2)设
| c2 |
| xy |
| k•xy |
∵
|
即
|
|
令
| x |
| y |
| 1 |
| t |
t+
|
t+
|
t+
|
t+
|
| 9 |
| 4 |
又∵
t+
|
t+
|
| 5 | ||||||||
|
| k |
得
| c2 |
| xy |
点评:本题考查的知识点是函数的值域,基本不等式在求函数最值时的应用,对勾函数的单调性,其中(1)的关键是将
的表达式,根据已知进行变形,为二次函数性质的应用或基本不等式的应用创造条件,(2)的关键是设
=k,并根据三角形的三边“任意两边之和大于第三边,任意两边之差小于第三边”构造关于k的不等式组.
| b |
| a |
| c2 |
| xy |

练习册系列答案
相关题目
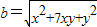 .
.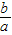 的取值范围;
的取值范围;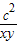 的取值范围.
的取值范围.