题目内容
若an=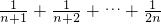 (n=1,2,3…),则an+1-an=________
(n=1,2,3…),则an+1-an=________

分析:由题意知,an+1-an=
 -(
-(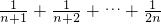 ),由此能够推陈出新出此结果.
),由此能够推陈出新出此结果.解答:an+1-an=
 -(
-(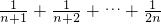 )
)=


=
 .
.故答案为:
 .
.点评:本题考查数列的运算,解题的关键是an+1=
 ,别丢掉
,别丢掉 这一项.
这一项. 
练习册系列答案
相关题目
题目内容
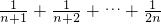 (n=1,2,3…),则an+1-an=________
(n=1,2,3…),则an+1-an=________
 -(
-(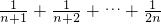 ),由此能够推陈出新出此结果.
),由此能够推陈出新出此结果. -(
-(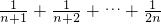 )
)

 .
. .
. ,别丢掉
,别丢掉 这一项.
这一项. 