题目内容
将椭圆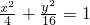
上的点的纵坐标不变，横坐标变为原来的2倍，则所得曲线的方程为________．
+
=1分析：设椭圆
+
=1上任意一点P（x0，y0），纵坐标不变，横坐标变为原来的2倍后的曲线上与P对应的点P′（x，y），依题意，可得点P与P′坐标之间的关系，通过代入法即可求得变化后所得曲线的方程．解答：设椭圆
+=1上任意一点P（x0，y0），纵坐标不变，横坐标变为原来的2倍后的曲线上与P对应的点P′（x，y），
则
，∴x0=
x，y0=y，∵P（x0，y0）为椭圆
+=1上任意一点将P（
x，y）代入椭圆+=1得：
+=1．故答案为：
+=1．点评：本题考查椭圆的简单性质，考查代入法的应用，得到点P与P′坐标之间的关系，是解决问题的关键，考查分析与转化的能力，属于中档题．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
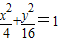上的点的纵坐标不变，横坐标变为原来的2倍，则所得曲线的方程为 ．
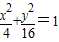上的点的纵坐标不变，横坐标变为原来的2倍，则所得曲线的方程为 ．
在M-1的作用下的新曲线的方程．
（t为参数），
（θ为参数）．
时，求C1与C2的交点坐标；
的最大值．
上各点的纵坐标不变，横坐标缩短为原来的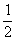
，得到一个椭圆，则该椭圆的离心率为
C．
D．