题目内容
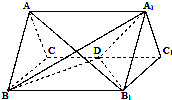 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点.(1)求证:AB1⊥平面A1BD;
(2)求三棱锥B-A1B1D的体积.
分析:(1)取BC中点E,连接B1E,证明BD⊥平面AEB1,得BD⊥AB1,由直线与平面垂直的判定定理,可得所证结论.
(2)连接B1D,则三棱锥B-A1B1D的体积可以通过求三棱锥A1-B1DB的体积得到.
(2)连接B1D,则三棱锥B-A1B1D的体积可以通过求三棱锥A1-B1DB的体积得到.
解答:(1)证明:由正三棱柱ABC-A1B1C1的所有棱长都相等可知:AB1⊥A1B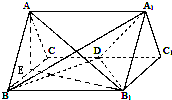
如图,取BC的中点E,连接B1E,则Rt△BCD≌Rt△B1BE
∴∠BB1E=∠CBD
∴∠CBD+∠BEB1=∠BB1E+∠BEB1=90°
∴BD⊥B1E
由平面ABC⊥平面BCC1B1,平面ABC∩平面BCC1B1=BC,且AE⊥BC得,AE⊥平面BCC1B1
∴AE⊥BD
∵B1E?平面AEB1,AE?平面AEB1,AE∩B1E=E
∴BD⊥平面AEB1
∴BD⊥AB1
∵A1B?平面A1BD,BD?平面A1BD,A1B∩BD=B
∴AB1⊥平面A1BD
(2)解:连接B1D,由AA1∥平面BCC1B1
所以点A1到平面BCC1B1的距离,等于AE=
=
=
S△BDB1=
S正方形BCC1B1=
×2×2=2
∴VB-A1B1D=VA1-BDB1=
×S△BDB1×AE=
×2×
=
故三棱锥B-A1B1D的体积为
.

如图,取BC的中点E,连接B1E,则Rt△BCD≌Rt△B1BE
∴∠BB1E=∠CBD
∴∠CBD+∠BEB1=∠BB1E+∠BEB1=90°
∴BD⊥B1E
由平面ABC⊥平面BCC1B1,平面ABC∩平面BCC1B1=BC,且AE⊥BC得,AE⊥平面BCC1B1
∴AE⊥BD
∵B1E?平面AEB1,AE?平面AEB1,AE∩B1E=E
∴BD⊥平面AEB1
∴BD⊥AB1
∵A1B?平面A1BD,BD?平面A1BD,A1B∩BD=B
∴AB1⊥平面A1BD
(2)解:连接B1D,由AA1∥平面BCC1B1
所以点A1到平面BCC1B1的距离,等于AE=
| AB2-BE2 |
| 22-12 |
| 3 |
S△BDB1=
| 1 |
| 2 |
| 1 |
| 2 |
∴VB-A1B1D=VA1-BDB1=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
故三棱锥B-A1B1D的体积为
2
| ||
| 3 |
点评:本题主要考查了线面垂直的判定定理、几何体体积的求法,解题过程中要注意各种位置关系的相互转化以及数量关系的求解.

练习册系列答案
相关题目
 如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )
如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )| A、2 | ||
B、
| ||
C、
| ||
D、
|
 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.