Question

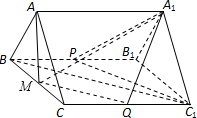
如图，正三棱柱ABC-A₁B₁C₁中（注：底面为正三角形且侧棱与底面垂直），BC=CC₁=2，P，Q分别为BB₁，CC₁的中点．
（Ⅰ）求多面体ABC-A₁PC₁的体积；
（Ⅱ）求A₁Q与BC₁所成角的大小．

Answer 1

分析：（I）要求多面体ABC-A₁PC₁的体积为三棱柱的体积减去三棱锥P-A₁B₁C₁的体积，分别求出棱柱与棱锥的体积，求差；
（II）取BC的中点M，连接MQ，可证∠MQA₁为异面直线所成的角，在△MQA₁中，分别求出三边长，利用余弦定理或勾股定理求角．

解答：解：（I）∵P为BB₁的中点，∴PB₁=1，
在正三棱柱ABC-A₁B₁C₁中，
VP-A1B1C1=

1

3

×

1

2

×2×2×

3

2

×1=

3

3

，
V_三棱柱=

1

2

×2×2×

3

2

×2=2

3

，
∴多面体ABC-A₁PC₁的体积V=2

3

-

3

3

=

5 3

3

．
（II）取BC的中点M，连接MQ，A₁M，AM，
则MQ∥BC₁，
∴∠MQA₁为异面直线A₁Q与BC₁所成的角，
在△MQA₁中，MQ=

1

2

BC₁=

2

；A₁Q=

4+1

=

5

，；AM=

3

，A₁M=

4+3

=

7

，
∴cos∠MQA₁=

2+5-7

2× 2 × 5

=0，
∴∠MQA₁=

π

2

．

点评：本题考查了几何法求异面直线所成的角，考查了用间接法求几何体的体积，体现了空间几何问题转化为平面几何问题这一基本解题思路．