题目内容
如图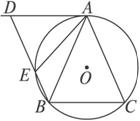
图
证明:∵AD是⊙O切线,
∴∠DAE=∠ABD.
∵BD∥AC,∴∠CAB=∠ABD.
∴∠DAE=∠CAB.∵∠AED=∠C,
∴△ADE∽△ABC.
∴∠D=∠ABC.
∵AB=AC,∴∠ABC=∠C.
∴∠D=∠AED.∴AD=AE.
∵AD2=DE·DB,
∴AE2=DE·DB.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
天天向上一本好卷系列答案小学生10分钟应用题系列答案题目内容
如图
图
证明:∵AD是⊙O切线,
∴∠DAE=∠ABD.
∵BD∥AC,∴∠CAB=∠ABD.
∴∠DAE=∠CAB.∵∠AED=∠C,
∴△ADE∽△ABC.
∴∠D=∠ABC.
∵AB=AC,∴∠ABC=∠C.
∴∠D=∠AED.∴AD=AE.
∵AD2=DE·DB,
∴AE2=DE·DB.
天天向上一本好卷系列答案小学生10分钟应用题系列答案
要制作一个如图的框架（单位：米），要求所围成的总面积为19.5（米2），其中ABCD是一个矩形，EFCD是一个等腰梯形，梯形高h=
