题目内容
已知曲线C:x=
(-2≤y≤2)和直线y=k(x-1)+3只有一个交点,求实数k的取值范围.
思路分析:恰当地作出图形是解本题的关键.将所给曲线和直线画在一个坐标系下,曲线为半圆,直线过定点,从图形中可以发现两者只有一个交点的情况.
解:如图4-2-11,曲线C表示是以(0,0)为圆心,2为半径的右半圆,直线过(1,3)点.
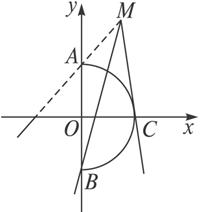
图4-2-11
由图可得kAM=
,kBM=
=5,
∴1≤k＜5.
又
=2,3k2+6k-5=0,解得k=-1±
(舍正).
∴k取值的集合为{k|1≤k＜5或k=-1-
}.
绿色通道:依据曲线交点的情况,寻求解析式中未知系数的取值范围问题,通常都借助于图象,数形结合会帮助我们迅速发现符合条件的部分图象,从而找到结果.
练习册系列答案
相关题目