题目内容
已知函数f(x)＝xlnx，过点A 
作函数y＝f(x)图象的切线，则切线的方程为________．
作函数y＝f(x)图象的切线，则切线的方程为________．x＋y＋
＝0
＝0设切点T(x0，y0)，则kAT＝f′(x0)，∴
＝lnx0＋1，即e2x0＋lnx0＋1＝0，设h(x)＝e2x＋lnx＋1，当x>0时h′(x)>0，∴h(x)是单调递增函数，∴h(x)＝0最多只有一个根．又h 
＝e2×＋ln＋1＝0，∴x0＝.由f′(x0)＝－1得切线方程是x＋y＋＝0.
＝lnx0＋1，即e2x0＋lnx0＋1＝0，设h(x)＝e2x＋lnx＋1，当x>0时h′(x)>0，∴h(x)是单调递增函数，∴h(x)＝0最多只有一个根．又h ＝e2×＋ln＋1＝0，∴x0＝.由f′(x0)＝－1得切线方程是x＋y＋＝0.
练习册系列答案
高中必刷题系列答案
相关题目
，其中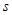
的单位是米，的单位是秒，那么物体在
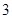秒末的瞬时速度是( )
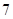米/秒
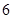米/秒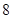
米/秒
米/秒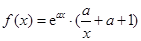
，其中
.
时，求曲线
在点
处的切线方程；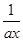
+b(a>0).
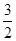x,求a,b的值.
处的切线方程是 
gt2，则从t＝0到t＝1时间段内的平均速度为________，在t＝1到t＝1＋Δt时间段内的平均速度________，在t＝1时刻的瞬时速度为________．